
分析 连结OA、OB,如图,根据切线的性质得∠OAP=∠OBP=90°,再利用四边形的内角和得到∠AOB=180°-∠P=140°,然后分类讨论:当点Q在优弧AB上,如图,根据圆周角定理可计算出∠AQB=$\frac{1}{2}$∠AOB=70°;当点Q弧AB上,如图,根据圆内接四边形的性质得∠AQ′B=180°-∠AQB=110°.
解答 解: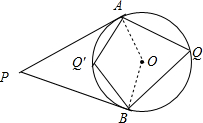 连结OA、OB,如图,
连结OA、OB,如图,
∵PA和PB为⊙O的两条切线,
∴OA⊥PA,PB⊥OB,
∴∠OAP=∠OBP=90°,
∴∠AOB=180°-∠P=180°-40°=140°,
当点Q在优弧AB上,如图,∠AQB=$\frac{1}{2}$∠AOB=70°;
当点Q弧AB上,如图,∠AQ′B=180°-∠AQB=180°-70°=110°,
综上所述,∠AQB的度数为70°或110.
故答案为70°或110.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了圆周角定理.


科目:初中数学 来源: 题型:选择题
 浙江卫视六频道《我老爸最棒》栏目中有一项”“大力金刚”的游戏.如图,有6根柱子穿过了一堵木墙,蓝、绿两队的两位老爸分别站在木墙的左、右两侧,需把自己一侧的那段柱子推向对方侧.若每侧每段柱子被选中的机会相等,则两人选到同一根柱子的概率为( )
浙江卫视六频道《我老爸最棒》栏目中有一项”“大力金刚”的游戏.如图,有6根柱子穿过了一堵木墙,蓝、绿两队的两位老爸分别站在木墙的左、右两侧,需把自己一侧的那段柱子推向对方侧.若每侧每段柱子被选中的机会相等,则两人选到同一根柱子的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{36}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
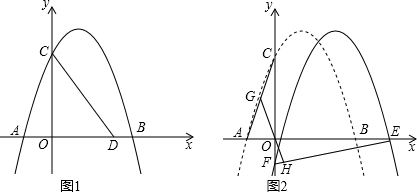
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
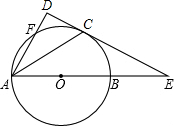 如图,已知AB是⊙O的直径,直线CE与⊙O相切于点C,交AB的延长线交于点E.作AD⊥CE,垂足为D,连接AC.求证:AC平分∠DAB.
如图,已知AB是⊙O的直径,直线CE与⊙O相切于点C,交AB的延长线交于点E.作AD⊥CE,垂足为D,连接AC.求证:AC平分∠DAB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
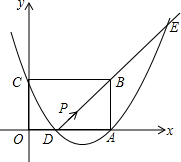 如图,已知矩形OABC,点A,C分别在x,y轴上,抛物线y=ax2+bx+c经过A(12,0),D(6,0)两点,且与y轴交于点C(0,8).动点P从点D出发,以每秒1个单位的速度沿射线DB方向运动,设P运动的时间为t(秒),射线DB交抛物线于E.
如图,已知矩形OABC,点A,C分别在x,y轴上,抛物线y=ax2+bx+c经过A(12,0),D(6,0)两点,且与y轴交于点C(0,8).动点P从点D出发,以每秒1个单位的速度沿射线DB方向运动,设P运动的时间为t(秒),射线DB交抛物线于E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
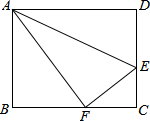 如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=10$\sqrt{5}$cm,且tan∠EFC=$\frac{3}{4}$,那么该矩形的周长为72cm.
如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=10$\sqrt{5}$cm,且tan∠EFC=$\frac{3}{4}$,那么该矩形的周长为72cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
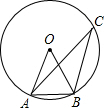 点B在⊙O上,点C是⊙O上异于A、B的一点,若∠AOB=50°,则∠ACB的度数是( )
点B在⊙O上,点C是⊙O上异于A、B的一点,若∠AOB=50°,则∠ACB的度数是( )| A. | 25° | B. | 65° | C. | 30° | D. | 25°、155° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com