
����Ŀ����֪��ƽ��ֱ������ϵxOy�У���ͼ������֪������y=��x2+bx+c������A��2��2�����Գ�����ֱ��x=1������ΪB��
��1�������������ߵı���ʽ�͵�B�����ꣻ
��2����M�ڶԳ����ϣ���λ�ڶ����Ϸ���������������Ϊm������AM���ú�m�Ĵ���ʽ��ʾ��AMB������ֵ��
��3���������������ϻ�����ƽ�ƣ�ʹ���������ߵĶ���C��x���ϣ�ԭ��������һ��Pƽ�ƺ�Ķ�Ӧ��Ϊ��Q�����OP=OQ�����Q�����꣮
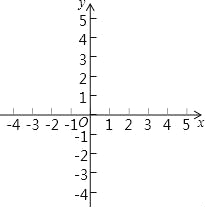
���𰸡���1�������ߵĽ���ʽΪy=��x2+2x+2������B����Ϊ��1��3����
��2��cot��AMB=m��2��
��3����Q��������![]() ����
����![]() ����
����![]() ����
����![]() ����
����
��������
�����������1�����������ߵĶԳ��᷽�̿����b��ֵ��Ȼ��A���������y=��x2+2x+c�����c��ֵ��
��2������A��AC��BM������ΪC���Ӷ��ɵõ�AC=1��MC=m��2���������������Ǻ����Ķ�����⼴�ɣ�
��3����ƽ�ƺ������ߵĶ�����x���Ͽ����ƽ�Ƶķ���;��룬�ʴ�QP=3��Ȼ���ɵ�QO=PO��QP��y��ɵõ���Q��P����x�Գƣ�����õ�Q�������꣬����Q�����������ƽ�ƺ�Ľ���ʽ����ö�Ӧ��x��ֵ����ɵõ���Q�����꣮
�����������1���������ߵĶԳ���Ϊx=1����x=��![]() =1����
=1����![]() =1�����b=2��
=1�����b=2��
��y=��x2+2x+c��
��A��2��2������ã���4+4+c=2����ã�c=2��
�������ߵĽ���ʽΪy=��x2+2x+2��
�䷽�ã�y=����x��1��2+3���������ߵĶ�������Ϊ��1��3����
��2����ͼ��ʾ������A��AC��BM������ΪC����AC=1��C��1��2����
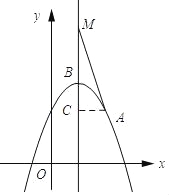
��M��1��m����C��1��2������MC=m��2����cot��AMB=![]() =m��2��
=m��2��
��3���������ߵĶ�������Ϊ��1��3����ƽ�ƺ������ߵĶ���������x���ϣ�
������������ƽ����3����λ��
��ƽ�ƺ������ߵĽ���ʽΪy=��x2+2x��1��PQ=3��
��OP=OQ������O��PQ�Ĵ�ֱƽ�����ϣ�
����QP��y�ᣬ����Q���P����x��Գƣ�
����Q����������![]() ��
��
��y=��![]() ����y=��x2+2x��1���x2+2x��1=��
����y=��x2+2x��1�ã���x2+2x��1=��![]() ����ã�x=
����ã�x=![]() ��x=
��x=![]() ��
��
����Q��������![]() ����
����![]() ����
����![]() ����
����![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��ͼ2��ͼ3��������״�ʹ�С��ȫ��ͬ�ķ���ֽ������ֽ��ÿ��С�����εı߳���Ϊ1��![]() ���㶼�ڸ���ϣ�����
���㶼�ڸ���ϣ�����![]() �������������ͼ��
�������������ͼ��
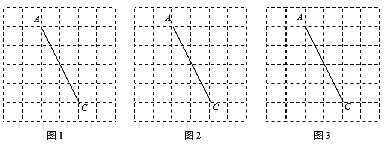
(1)��![]() Ϊ�Խ�����ͼ1����һ�������Σ��������θ�������ڸ����.
Ϊ�Խ�����ͼ1����һ�������Σ��������θ�������ڸ����.
(2)��![]() Ϊ�Խ�����ͼ2����һ�����Σ�ʹ�þ������Ϊ6���Ҿ��θ�������ڸ����.
Ϊ�Խ�����ͼ2����һ�����Σ�ʹ�þ������Ϊ6���Ҿ��θ�������ڸ����.
(3)��![]() Ϊ�Խ�����ͼ3����һ�������С��ƽ���ı��Σ���ƽ���ı��θ�������ڸ����.
Ϊ�Խ�����ͼ3����һ�������С��ƽ���ı��Σ���ƽ���ı��θ�������ڸ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���E����FΪ�Խ���BD�����ȷֵ㣬����E����F��BD��ֱ��ֱ�߷ֱ�AB��BC��AD��DC�ڵ�M��N��P��Q��MF��PE���ڵ�R��NF��EQ���ڵ�S����֪�ı���RESF�����Ϊ5cm2��������ABCD������ǣ�������
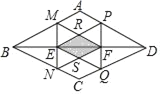
A. 35cm2B. 40cm2C. 45cm2D. 50cm2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�ADƽ�֡�BAC��BC�ڵ�D��DE��AB�ڵ�E��DF��AC�ڵ�F����MDN�����߷ֱ���AB��AC�ཻ��M��N���㣬�ҡ�MDN+��BAC��180�㣮
��1����֤AE��AF��
��2����AD��6��DF��2![]() �����ı���AMDN�������
�����ı���AMDN�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c�������������϶�Ӧ���λ����ͼ��ʾ�����м����жϣ���a<c<b����-a<b����a+b>0����c-a<0����a+c>0����![]() ����ȷ�ĸ�����( )
����ȷ�ĸ�����( )
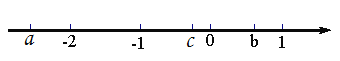
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���������AB������һ��̨CD��̨��ÿ���0.3�ף���AC=17�ף�����һֻС��˯��̨��FG�⣬����ɹ̫������̫��������ˮƽ����ļн�Ϊ��������=60��ʱ����ù����AB�ڵ����ϵ�Ӱ��AE=10�ף�����һ�ᣬ����=45������С����FG����Ƿ���ɹ��̫������˵�����ɣ�![]() ȡ1.73����
ȡ1.73����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
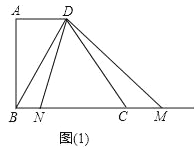
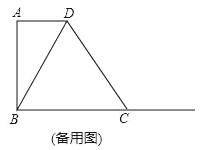
����Ŀ����֪��������ABCD�У�AD��BC����A=90�㣬AD=2��AB=4��BC=5��������BC��ȡһ��M������DM������MDN=��BDC����MDN����һ��DN��ֱ��BC�ڵ�N����N�ڵ�M����ࣩ��
��1����BM�ij�Ϊ10ʱ����֤��BD��DM��
��2����ͼ��1��������N���߶�BC��ʱ����BN=x��BM=y����y����x�ĺ�����ϵʽ����д�����Ķ�����
��3�������DMN�ǵ��������Σ���BN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������OABC����B������Ϊ��8��3��������D������Ϊ��12��0��������P�ӵ�O��������ÿ��2����λ���ȵ��ٶ���x��������������˶�������Q�ӵ�D��������ÿ��1����λ���ȵ��ٶ���x��ĸ����������˶���PQ����ͬʱ�˶�������ʱֹͣ�����˶������У���PQΪб����x���Ϸ�������ֱ��������PQR�����˶�ʱ��Ϊt�룮
��1����t=�� ��ʱ����PQR�ı�QR������B��
��2������PQR�;���OABC�ص����ֵ����ΪS����S����t�ĺ�����ϵʽ��
��3����ͼ2��������E��5��0����EF��BC������ΪF������PQR�Ķ���R���ھ���OABC���ڲ�ʱ������R��x�ᡢy���ƽ���ߣ��ֱ�EF��BC�ڵ�M��N������MAN=45������t��ֵ��
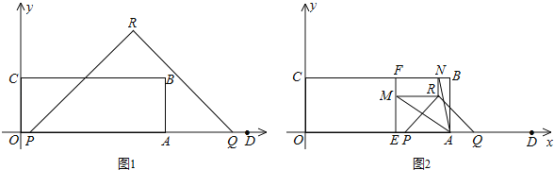
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ɽˮ�������кס��������зֱ���60000Ԫ����ͬ�Ľ��۹�����ͬ������ˮ���ң��׳������۷����ǣ���ˮ���Ұ������װ���ۣ������������ʴ����ˮ����400�䣬�Խ��۵�2���۸����ۣ�ʣ�µ�ˮ�����Ը��ڽ���10%���ۣ��ҳ��е����۷����ǣ�����ˮ���ҷ��ֱ࣬�����ۣ��۸׳��з������۵�����ˮ�����ۼ۵�ƽ�������ۣ��������н�ˮ����ȫ�����꣬���м׳��л���42000Ԫ(�����ɱ�����)���ʣ�
(1)ˮ���ҽ���Ϊÿ�����Ԫ��
(2)�ҳ��л�������Ԫ���������۷�ʽ�����㣿
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com