
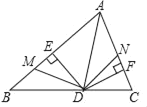
【题目】如图,在△ABC中,AD平分∠BAC交BC于点D,DE⊥AB于点E,DF⊥AC于点F,∠MDN的两边分别与AB,AC相交于M,N两点,且∠MDN+∠BAC=180°.
(1)求证AE=AF;
(2)若AD=6,DF=2![]() ,求四边形AMDN的面积.
,求四边形AMDN的面积.

【答案】(1)详见解析;(2)![]()
【解析】
(1)依据HL判定Rt△ADE≌Rt△ADF,即可得出AE=AF;
(2)判定△DEM≌△DFN,可得S△DEM=S△DFN,进而得到S四边形AMDN=S四边形AEDF,求得S△ADF=![]() AF×DF=2
AF×DF=2![]() ,即可得出结论.
,即可得出结论.
(1)∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,
∴DE=DF,
又∵DE⊥AB于点E,DF⊥AC于点F,
∴∠AED=∠AFD=90°,
又∵AD=AD,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF;
(2)∵∠MDN+∠BAC=180°,
∴∠AMD+∠AND=180°,
又∵∠DNF+∠AND=180°
∴∠EMD=∠FND,
又∵∠DEM=∠DFN,DE=DF,
∴△DEM≌△DFN,
∴S△DEM=S△DFN,
∴S四边形AMDN=S四边形AEDF,
∵AD=6,DF=2![]() ,
,
∴Rt△ADF中,AF=![]()
∴![]()
∴![]()
![]()


科目:初中数学 来源: 题型:
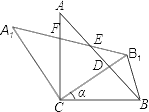
【题目】如图,△ABC中,∠ACB=90,AC=BC,将△ABC绕点C逆时针旋转α角(0<α<90)得到△A1B1C,连结BB1.设CB1交AB于D,A1B1分别交AB、AC于E、F,
(1)在图中不再添加其它任何线段的情况下,请你找出一对全等的三角形,并加以证明(△ABC与△A1B1C全等除外);
(2)当△BB1D是等腰三角形时,求α.
查看答案和解析>>
科目:初中数学 来源: 题型:
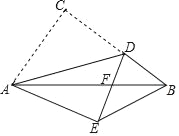
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() .求BE的长.
.求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当△DEB是直角三角形时,DF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
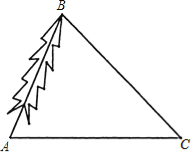
【题目】为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,求这棵古杉树AB的长度.(结果取整数)
参考数据:![]() ≈1.41,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30.
≈1.41,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中(如图),已知抛物线y=﹣x2+bx+c经过点A(2,2),对称轴是直线x=1,顶点为B.
(1)求这条抛物线的表达式和点B的坐标;
(2)点M在对称轴上,且位于顶点上方,设它的纵坐标为m,联结AM,用含m的代数式表示∠AMB的余切值;
(3)将该抛物线向上或向下平移,使得新抛物线的顶点C在x轴上.原抛物线上一点P平移后的对应点为点Q,如果OP=OQ,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
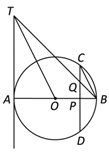
【题目】如图,AB是⊙O的直径,AT是经过点A的切线,弦CD垂直AB于P点,Q为线段CP的中点,连接BQ并延长交切线AT于T点,连接OT.
(1)求证:BC∥OT;
(2)若⊙O直径为10,CD=8,求AT的长;
(3)延长TO交直线CD于R,若⊙O直径为10,CD=8,求TR的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点A、B、O在数轴上对应的数为a、b、0,且满足|a+8|+(b﹣12)2=0,点M、N分别从O、B出发,同时向左匀速运动,M的速度为1个单位长度每秒,N的速度为3个单位长度每秒,A、B之间的距离定义为:AB=|a﹣b|.
(1)直接写出OA= .OB= ;
(2)设运动的时间为t秒,当t为何值时,恰好有AN=2AM;
(3)若点P为线段AM的中点,Q为线段BN的中点,M、N在运动的过程中,PQ+MN的长度是否发生变化?若不变,请说明理由,若变化,当t为何值时,PQ+MN有最小值?最小值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com