
【题目】如图,边长为 2 的正方形 OABC 顶点 O 与坐标原点 O 重合,边 OA、OC 分别与 x、y 正半轴重合, 在 x 轴上取点 P(﹣2,0),将正方形 OABC 绕点 O 逆时针旋转 a°(0°<a<180°),得到正方形 OA′B′C′,在旋转过程中,使得以 P,A′,B′为顶点的三角形是等腰三角形时,点 A′的坐标是_______.

【答案】(![]() ,1)或(0,2)或(1,
,1)或(0,2)或(1,![]() )或(
)或(![]() ,1)
,1)
【解析】
分四种情形:①当PB′=PA′时,②当A′与C重合时,③当PA′=A′B′时,④当PA′=PB′时,分别画出图形求解即可得到A′的坐标.
解:有四种情况:
①如图1中,当PB′=PA′时,连接PC′.易证△POC′是等边三角形,
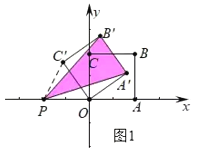
∴∠POA′=150°,∠A′OA=30°,
∵OA′=2,
∴A′(![]() ,1);
,1);
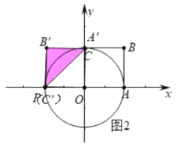
②如图2中,当A′与C重合时,△PA′B′是等腰三角形,此时A′(0,2);
③如图3中,当PA′=A′B′时,△A′OP是等边三角形,
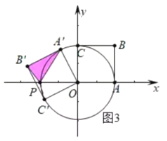
∴∠A′OP=60°,
∴A′(1,![]() );
);
④如图4中,当PA′=PB′时,易证△POC′是等边三角形,
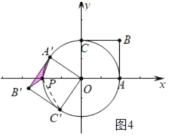
∴∠POC′=60°,
∵∠A′OC′=90°,
∴∠A′OP=30°,
∵OA′=2,
∴A′(![]() ,1),
,1),
综上所述,满足条件的点A′坐标为(![]() ,1)或(0,2)或(1,
,1)或(0,2)或(1,![]() )或(
)或(![]() ,1).
,1).
故答案为:(![]() ,1)或(0,2)或(1,
,1)或(0,2)或(1,![]() )或(
)或(![]() ,1).
,1).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=![]() ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索: ![]() 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示.
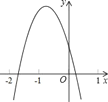
下列结论:①abc>0;②2a﹣b<0;③4a﹣2b+c<0;④(a+c)2<b2其中正确的个数有( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一列数![]() ,a2,a3,…,
,a2,a3,…,![]() ,其中a1=-1,
,其中a1=-1,![]() ,
,![]() ,…,
,…,![]() ,完成下列填空:
,完成下列填空:
(1)a2 = ,a3 = ,a2019 = ;
(2)a1+a2+a3+……+a2019 = .(直接写出计算结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画出直线![]() 的图象,并解答下列问题:
的图象,并解答下列问题:
(1)设它的图象与y轴、x轴分别交于点A、B,求AB的长;
(2)求![]() 的周长(O为坐标原点);
的周长(O为坐标原点);
(3)求点O到直线AB的距离;
(4)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E、F分别在AB、BC上,且AE=BF=1,CE、DF交于点O,下列结论:①∠DOC=90°,②OC=OE,③CE=DF,④tan∠OCD=![]() ,⑤S△DOC=S四边形EOFB中,正确的有( )
,⑤S△DOC=S四边形EOFB中,正确的有( )
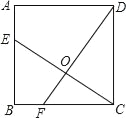
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=2x+4
(1)在如图所示的平面直角坐标系中,画出函数的图象;

2)求图象与x轴的交点A的坐标,与y轴交点B的坐标;
(3)在(2)的条件下,求出△AOB的面积;
(4)利用图象直接写出:当y<0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1) (-![]() )-(+
)-(+![]() )+(-8)-(+3); (2)
)+(-8)-(+3); (2) ![]()
(3) ![]() (4) (1)-22 -(1-
(4) (1)-22 -(1-![]() ×0.2)÷(-2)3
×0.2)÷(-2)3
(5)a2-3a+8-3a2+4a-6 (6) ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com