
����Ŀ��������ABCD��������AEFG�й�������A����������AEFG�Ƶ�A��˳ʱ�뷽����ת������ת�ǡ�DAG=��������0��ܦ���180�㣬����DF��BF����ͼ�� 
��1������=0�㣬��DF=BF�������֤����
��2���Ի�һ��ͼ�Σ�����������˵����1����������������Ǽ����⣻
��3�����ڣ�1��������������⣬����ܲ���һ����������ʹ��������Ϊ�����⣬��ֱ��д������Ϊ��Ҫ�����һ������������˵�����ɣ�
���𰸡�
��1��֤������ͼ1�����ı���ABCD���ı���AEFGΪ�����Σ�
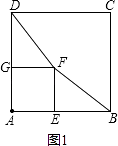
��AG=AE��AD=AB��GF=EF����DGF=��BEF=90�㣬
��DG=BE��
�ڡ�DGF�͡�BEF�У�
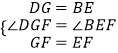 ��
��
���DGF�ա�BEF��SAS����
��DF=BF
��2���⣺ͼ�Σ�����������ͼ2��
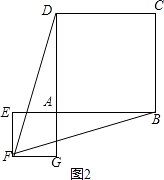
��3���⣺����һ������Ϊ����F��������ABCD�ڣ�
��������F��������ABCD�ڣ�DF=BF������ת�Ǧ�=0��
����������1�����������ε�����֤����DGF�ա�BEF���ɣ���2������=180��ʱ��DF=BF����3�����������ε����ʺ͡�DGF�ա�BEF�����ʼ���֤���������⣮
�����㾫����ͨ��������������ε����ʺ������붨���������������ĸ��Ƕ���ֱ�ǣ������߶���ȣ������ε������Խ�����ȣ����һ��ഹֱƽ�֣�ÿ���Խ���ƽ��һ��Խǣ������ε�һ���Խ��߰������ηֳ�����ȫ�ȵĵ���ֱ�������Σ������εĶԽ�����ߵļн���45o�������ε������Խ��߰���������ηֳ��ĸ�ȫ�ȵĵ���ֱ�������Σ����ǰ����衢���������෴��������������������⣮���������һ������ԭ���⣬��ô��һ���������������⣻����֤����ȷ����ȷ������������������Խ����⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����A=30�㣬AB�Ĵ�ֱƽ����l��AC�ڵ�D�����CBD�Ķ���Ϊ�� �� 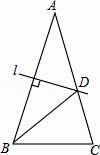
A.30��
B.45��
C.50��
D.75��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1�ǡ�����ֱ֪�������ε����Բ���ij߹���ͼ����
��֪��Rt��ABC����C=90�㣬����Rt��ABC�����Բ��
��������ͼ2��
��1���ٷֱ��Ե�A�͵�BΪԲ�ģ����� ![]() �ij�Ϊ�뾶�����������ཻ��P��Q���㣻
�ij�Ϊ�뾶�����������ཻ��P��Q���㣻
����ֱ��PQ����AB�ڵ�O��
��2����OΪԲ�ģ�OAΪ�뾶����O����O��Ϊ��������Բ��
��ش𣺸ó߹���ͼ�������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�콫�ʼDZ�����ˮƽ�����������ϣ���ʾ��OB��װ�OA����ˮƽ�ߵļн�Ϊ120�㣬�о������ʣ���ͼ1��������ʾ��ͼΪͼ2��ʹ��ʱΪ��ɢ�ȣ����ڵװ��µ���ɢ�ȼ�ACO�����ת��AO��B��λ�ã���ͼ3��������ʾ��ͼΪͼ4����֪OA=OB=24cm��O��C��OA�ڵ�C��O��C=12cm�� 
��1�����CAO��Ķ�����
��2����ʾ���Ķ���B���ԭ�������˶��٣�
��3����ͼ4������ɢ�ȼܺ�Ҫʹ��ʾ��O��B��ˮƽ�ߵļн��Ա���120�㣬����ʾ��O��B��Ӧ�Ƶ�O�䰴˳ʱ�뷽����ת���ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڡ�ACB�͡�AED�У�AC=BC��AE=DE����ACB=��AED=90�㣬��E��AB�ϣ�F���߶�BD���е㣬����CE��FE��
��1����AD=3 ![]() ��BE=4����EF�ij���
��BE=4����EF�ij���
��2����֤��CE= ![]() EF��
EF��
��3����ͼ1�еġ�AED�Ƶ�A˳ʱ����ת��ʹAED��һ��AEǡ�����ACB�ı�AC��ͬһ��ֱ���ϣ���ͼ2��������BD��ȡBD���е�F���ʣ�2���еĽ����Ƿ���Ȼ��������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y=ax2+bx+c��x�ύ��A��B���㣬��y�ύ��������C�㣬��AC=20��BC=15����ACB=90�㣬��������ߵĽ���ʽΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABCD����ͼ���Ƶ�A��ת��D���ڱ�AB�ϵĵ�D�䣬��C�䵽C�䣬�ҵ�C�䡢B��C��һֱ���ϣ����AB=13��AD=3����ô��A������ֵΪ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����MON=20�㣬A��B�ֱ�Ϊ����OM��ON�������㣬��OA=2��OB=4����P��Q�ֱ�Ϊ����OM��ON�����㣬��P��Q�˶�ʱ���߶�AQ+PQ+PB����Сֵ�ǣ� �� 
A.3
B.3 ![]()
C.2
D.2 ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com