
【题目】已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.
问题发现
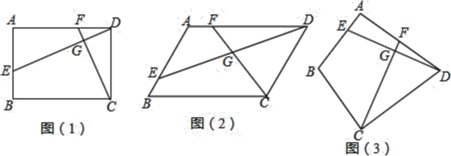
![]() 如图
如图![]() ,若四边形ABCD是矩形,且
,若四边形ABCD是矩形,且![]() 于G,
于G,![]() ,填空:
,填空:![]() ______;
______;![]() 当矩形ABCD是正方形时,
当矩形ABCD是正方形时,![]() ______;
______;
拓展探究
![]() 如图
如图![]() ,若四边形ABCD是平行四边形,试探究:当
,若四边形ABCD是平行四边形,试探究:当![]() 与
与![]() 满足什么关系时,
满足什么关系时,![]() 成立?并证明你的结论;
成立?并证明你的结论;
解决问题
![]() 如图
如图![]() ,若
,若![]() 于G,请直接写出
于G,请直接写出![]() 的值.
的值.
【答案】(1)①![]() ,②1;(2)当
,②1;(2)当![]() +
+![]() =180°时,
=180°时,![]() 成立,理由见解析;(3)
成立,理由见解析;(3)![]() .
.
【解析】
(1)根据矩形的性质先一步证明△AED~△DFC,然后进一步利用相似三角形性质求解即可;
(2)在AD的延长线上取一点M,使得CM=CF,则∠CMD=∠CFM,通过证明△ADE~△DCM进一步求解即可;
(3)过C点作CN⊥AD于N点,CM⊥AB交AB延长线于M点,连接BD,先证明△BAD≌△BCD,然后进一步证明△BCM~△DCN,再结合勾股定理求出CN,最终通过证明△AED~△NFC进一步求解即可.
(1)∵四边形ABCD为矩形,
∴∠A=∠FDC=90°,AB=CD,
∵CF⊥DE,
∴∠DGF=90°,
∴∠ADE+∠CFD=90°,
∠ADE+∠AED=90°,
∴∠CFD=∠AED,
∵∠A=∠CDF,
∴△AED~△DFC,
∴![]() ,
,
∴①![]() ,②若四边形ABCD为正方形,
,②若四边形ABCD为正方形,![]() ,
,
故答案为:①![]() ,②1;
,②1;
(2)当![]() +
+![]() =180°时,
=180°时,![]() 成立,理由如下:
成立,理由如下:
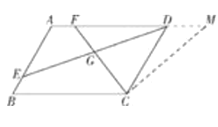
如图,在AD的延长线上取一点M,使得CM=CF,则∠CMD=∠CFM,
∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC,
∴∠A=∠CDM,
∵∠B+∠EGC=180°,
∴∠BEG+∠FCB=180°,
∵∠BEG+∠AED=180°,
∴∠AED=∠FCB,
∵AD∥BC,
∴∠CFM=∠FCB,
∴∠CMD=∠AED,
∴△ADE~△DCM,
∴![]() ,
,
即:![]() ;
;
(3)![]() ,理由如下:
,理由如下:
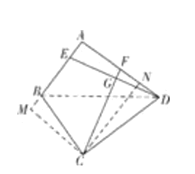
过C点作CN⊥AD于N点,CM⊥AB交AB延长线于M点,连接BD,设CN=x,
∵∠BAD=90°,即AB⊥AD,
∴∠A=∠M=∠CAN=90°,
∴四边形AMCN为矩形,
∴AM=CN,AN=CM,
在△BAD与△BCD中,
∵AD=CD,AB=BC,BD=BD,
∴△BAD≌△BCD(SSS),
∴∠BCD=∠A=90°,
∴∠ABC+∠ADC=180°,
∵∠ABC+∠CBM=180°,
∴∠MBC=∠ADC,
∵∠CND=∠M=90°,
∴△BCM~△DCN,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在Rt△CMB中,![]() ,BM=AMAB=
,BM=AMAB=![]() ,
,
由勾股定理可得:![]() ,
,
∴![]() ,
,
解得:![]() (舍去)或
(舍去)或![]() ,
,
∴![]() ,
,
∵∠A=∠FGD=90°,
∴∠AED+∠AFG=180°,
∵∠AFG+∠NFC=180°,
∴∠AED=∠CFN,
∵∠A=∠CNF,
∴△AED~△NFC,
∴![]() .
.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一段时间后,记录下这种植物高度的增长情况(如下表):
温度x/℃ | … | ﹣4 | ﹣2 | 0 | 2 | 4 | 6 | … |
植物每天高度的增长量y/mm | … | 41 | 49 | 49 | 41 | 25 | 1 | … |
由这些数据,科学家推测出植物每天高度的增长量y是温度x的二次函数,那么下列三个结论:
①该植物在0℃时,每天高度的增长量最大;
②该植物在﹣6℃时,每天高度的增长量能保持在25mm左右;
③该植物与大多数植物不同,6℃以上的环境下高度几乎不增长.
上述结论中,所有正确结论的序号是
A. ①②③ B. ①③ C. ①② D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
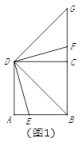
【题目】⑴如图1,![]() 是正方形
是正方形![]() 边
边![]() 上的一点,连接
上的一点,连接![]() ,将
,将![]() 绕着点
绕着点![]() 逆时针旋转90°,旋转后角的两边分别与射线
逆时针旋转90°,旋转后角的两边分别与射线![]() 交于点
交于点![]() 和点
和点![]() .
.
①线段![]() 和
和![]() 的数量关系是 ;
的数量关系是 ;
②写出线段![]() 和
和![]() 之间的数量关系.
之间的数量关系.
⑵当四边形![]() 为菱形,
为菱形,![]() ,点
,点![]() 是菱形
是菱形![]() 边
边![]() 所在直线上的一点,连接
所在直线上的一点,连接![]() ,将
,将![]() 绕着点
绕着点![]() 逆时针旋转120°,旋转后角的两边分别与射线
逆时针旋转120°,旋转后角的两边分别与射线![]() 交于点
交于点![]() 和点
和点![]() .
.
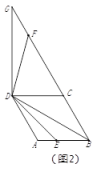
①如图2,点![]() 在线段上时,请探究线段
在线段上时,请探究线段![]() 和
和![]() 之间的数量关系,写出结论并给出证明;
之间的数量关系,写出结论并给出证明;
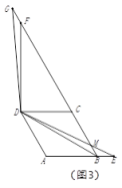
②如图3,点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() 交射线
交射线![]() 于点
于点![]() ;若
;若 ![]() ,直接写出线段
,直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
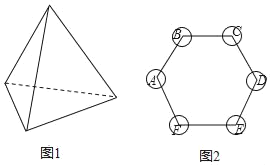
【题目】图①是一枚质地均匀的正四面体形状的骰子,每个面上分别标有数字2,3,4,5.图②是一个正六边形棋盘,现通过掷骰子的方式玩跳棋游戏,规则是:将这枚骰子在桌面掷出后,看骰子落在桌面上(即底面)的数字是几,就从图中的A点开始沿着顺时针方向连续跳动几个顶点,第二次从第一次的终点处开始,按第一次的方法继续……
(1)随机掷一次骰子,则棋子跳动到点C处的概率是 .
(2)随机掷两次骰子,用画树状图或列表的方法,求棋子最终跳动到点C处的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”假期,成都某公司组织部分员工分别到甲、乙、丙、丁四地考察,公司按定额购买了前往各地的车票,如图是用来制作完整的车票种类和相应数量的条形统计图,根据统计图回答下列问题:
![]() 若去丙地的车票占全部车票的
若去丙地的车票占全部车票的![]() ,则总票数为______ 张,去丁地的车票有______ 张
,则总票数为______ 张,去丁地的车票有______ 张![]()
![]() 若公司采用随机抽取的方式发车票,小胡先从所有的车票中随机抽取一张
若公司采用随机抽取的方式发车票,小胡先从所有的车票中随机抽取一张![]() 所有车票的形状、大小、质地完全相同、均匀
所有车票的形状、大小、质地完全相同、均匀![]() ,那么员工小胡抽到去甲地的车票的概率是多少?
,那么员工小胡抽到去甲地的车票的概率是多少?
![]() 若有一张车票,小王和小李都想要,他们决定采取掷一枚质地均匀的正方体骰子的方式来确定给谁,其上的数字是3的倍数,则给小王,否则给小李
若有一张车票,小王和小李都想要,他们决定采取掷一枚质地均匀的正方体骰子的方式来确定给谁,其上的数字是3的倍数,则给小王,否则给小李![]() 请问这个规则对双方是否公平?若公平请说明理由;若不公平,请通过计算说明对谁更有利.
请问这个规则对双方是否公平?若公平请说明理由;若不公平,请通过计算说明对谁更有利.

查看答案和解析>>
科目:初中数学 来源: 题型:
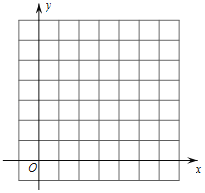
【题目】如图,在正方形网格中,每个小正方形的边长为1,点A(1,5)、B(6,5)、C(2,3)、D(1,4).
(1)画出△ABC,并判断出△ABC的形状;
(2)将线段AB绕点P逆时针旋转90°得到线段AE,其中点B的对应点为点A,点A的对应点为点E,写出P点的坐标;
(3)连接BD,交AC于点M,则![]() 的比值为 (直接写出结果).
的比值为 (直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
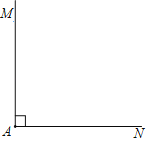
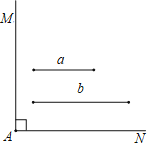
【题目】已知:如图,∠MAN=90°,线段a和线段b
求作:矩形ABCD,使得矩形ABCD的两条边长分别等于线段a和线段b.
下面是小东设计的尺规作图过程.
作法:如图,
①以点A为圆心,b为半径作弧,交AN于点B;
②以点A为圆心,a为半径作弧,交AM于点D;
③分别以点B、点D为圆心,a、b长为半径作弧,两弧交于∠MAN内部的点C;
④分别连接BC,DC.
所以四边形ABCD就是所求作的矩形.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:
∵AB= ;AD= ;
∴四边形ABCD是平行四边形.
∵∠MAN=90°;
∴四边形ABCD是矩形( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
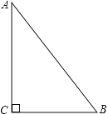
【题目】如图,△ABC中,∠C=90°,AC=4cm,BC=3cm,若动点P从点C开始,沿C→A→B→C的路径运动一周,且速度为每秒2cm,设运动时间为t秒,当t=_____时,点P与△ABC的某两个顶点构成等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com