

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 一个门框的尺寸如图所示:
一个门框的尺寸如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数),那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时,它们之间的距离是$\sqrt{2}$.
如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数),那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时,它们之间的距离是$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
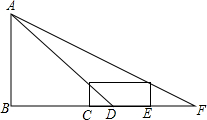 如图,小明同学晚上由路灯A下的B处走到C处时,测的影子CD的长为1.5米,继续往前走3米到达E处时,测的影子EF的长为2.5米,已知小明同学的身高是1.5米,求路灯AB的高度.
如图,小明同学晚上由路灯A下的B处走到C处时,测的影子CD的长为1.5米,继续往前走3米到达E处时,测的影子EF的长为2.5米,已知小明同学的身高是1.5米,求路灯AB的高度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,D为BC上一点,E为AD延长线上一点,BD:DC=5:3,∠C=∠E,若AD=4,BC=8,则DE的长为( )
如图,在△ABC中,D为BC上一点,E为AD延长线上一点,BD:DC=5:3,∠C=∠E,若AD=4,BC=8,则DE的长为( )| A. | $\frac{15}{4}$ | B. | $\frac{15}{3}$ | C. | 5 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,A、B、C是同一直线上的依次三点,下列说法正确的是( )
如图所示,A、B、C是同一直线上的依次三点,下列说法正确的是( )| A. | 射线AB与射线BA是同一条射线 | B. | 射线BA与射线BC是同一条射线 | ||
| C. | 射线AB与射线AC是同一条射线 | D. | 直线BA与直线BC不是同一条直线 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形纸片ABCD中,AD∥BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C′处,折痕DE交BC于点E,连结C′E.
如图,在四边形纸片ABCD中,AD∥BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C′处,折痕DE交BC于点E,连结C′E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com