练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    某中学九年级一位同学不幸得了重病，牵动了全校师生的心，该校开展了“献爱心”捐款活动.第一天收到捐款10 000元，第三天收到捐款12 100元.

    (1) 如果第二天、第三天收到捐款的增长率相同，求捐款增长率；

    (2) 按照(1)中收到捐款的增长速度，第四天该校能收到多少捐款？


    (1)设第二、三两天捐款增长率为x         

    根据题意列方程得，10000×(1+x)2=12100，(3分)

    解得x1=0.1，x2=﹣2.1(不合题意，舍去)．(5分)             

    答：第二、三两天捐款的增长率为10%．  (6分)

    (2) 12100×(1+0.1)=13310(元)

    答：第四天该校收到的捐款为13310元．(8分)


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


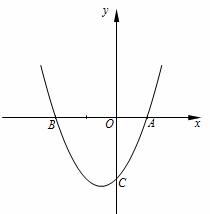
    已知二次函数y＝ax2＋bx＋c（a＞0）的图像与x轴的一个交点为A（1，0），另一个交点为B，与y轴的交点为C（0，－2）．

    （1）b＝，点B的坐标为（        ，        ）    ；（均用含a的代数式表示）

    （2）若a＜2，试证明二次函数图像的顶点一定在第三象限；

    （3）若a＝1，点P是抛物线在x轴下方的一个动点（不与C重合），连结PB，PC，设所得△PBC的面积为S，试求S的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，点M，N分别是正五边形ABCDE的边BC，CD上的点，且BM＝CN，AM交BN于点P.

    （1）求证：AM＝BN；

    （2）求∠APN的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某排球队12名队员的年龄如下表所示：

    年龄/岁

    19

    20

    21

    22

    23

    人数/人

    1

    5

    3

    1

    2

    则该队队员年龄的中位数是            .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知：在平面直角坐标系xoy中，抛物线y=ax2＋bx＋c与直线y=mx＋n相交于

    A(0，－),B(m－b，m2－mb＋n)两点,其中a，b，c，m，n均为实数，且a≠0，m≠0

    (1) ①填空：c=        ，n=        ；

    ②求a的值。

    小明思考：∵B(m－b，m2－mb＋n) 在抛物线y=ax2＋bx＋c上

    ∴m2－mb＋n=a(m－b)2+b(m－b)+c

    ……

    请根据小明的解题过程直接写出a 的值：a = ___________.

    (2) 若m=1，b=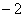,设点P在抛物线y=ax2＋bx＋c上，且在直线AB的下方，求△ABP

    面积的取值范围；

    (3) 当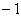 ≤ x ≤1时，求抛物线y=ax2＋bx＋c上到x轴距离最大的点的坐标。（用含b的代数式表示）

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若不等式组 有解，则实数a的取值范围是（　　）

    　  A．a＜4       B． a≤4      C．a＞4       D．a≥4

    查看答案和解析>>

    科目：初中数学 来源： 题型：


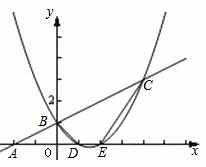
    已知：如图，一次函数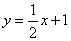的图像与x轴交于点A，与y轴交于点B，二次函数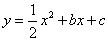的图像与一次函数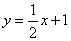的图像相交于B、C两点，与x轴

    交于D、E两点且D点坐标为（1，0）.

    （1）求二次函数的解析式；

    （2）求四边形BDEC的面积S；

    （3）在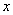轴上是否存在点P.，使△PBC是以P为直角顶点的直角三角

    形？若存在，求出所有的点P的坐标，若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    学校篮球集训队11名队员进行定点投篮训练，11名队员在1分钟内投进篮框的球数和人数如下表：

    则11名队员投进篮框的球数的中位数是_______个．

    查看答案和解析>>

    同步练习册答案