练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

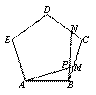
    如图，点M，N分别是正五边形ABCDE的边BC，CD上的点，且BM＝CN，AM交BN于点P.

    （1）求证：AM＝BN；

    （2）求∠APN的度数.


    解：（1）证明：∵五边形ABCDE为正五边形，∴AB＝BC，∠ABM＝∠C，在△ABM和△BCN中，∵,∴△ABM≌△BCN（SAS），∴AM＝BN.

    （2）由（1）得△ABM≌△BCN，∴∠BAM＝∠CBN，∵∠BAM＋∠ABP＝∠APN，∴∠CBN＋∠ABP＝∠APN＝∠ABC＝，∴∠APN的度数为108°.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


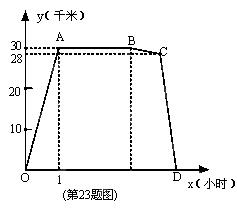
    周六上午8：00小明从家出发，乘车1小时到郊外某基地参加社会实践活动，在基地活动2.2小时后，因家里有急事，他立即按原路以4千米/时的平均速度步行返回．同时爸爸开车从家出发沿同一路线接他，在离家28千米处与小明相遇。接到小明后保持车速不变，立即按原路返回．设小明离开家的时间为x小时，小名离家的路程y (干米) 与x (小时)之间的函致图象如图所示，

    (1)小明去基地乘车的平均速度是________千米/小时，爸爸开车的平均速度应是________千米/小时；

    (2)求线段CD所表示的函敛关系式；

    (3)问小明能否在12：0 0前回到家？若能，请说明理由：若不能，请算出12：00时他离家的路程，

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    小王同学想知道学校旗杆的高，他发现从旗杆顶上挂下来的绳子垂直到地面还多1米（如图12），当他把绳子拉开离旗杆底部5米后，绳子下端刚好接触地面，则学校旗杆高度为           ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


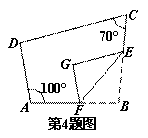
    如图，在四边形ABCD中，点F，E分别在边AB，BC上，将△BFE沿FE翻折，得△GFE，若GF∥AD，GE∥DC，则∠B的度数为……………………………………【   】

    A.95°               B.100°              C.105°             D.110°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    化简的结果______________________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


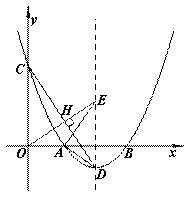
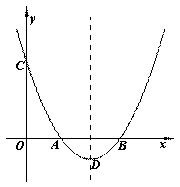
    如图，抛物线y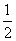＝(x－3)2－1与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，顶点为D.

    （1）试求点A、B、D的坐标；

    （2）连接CD，过原点O作OE⊥CD于点H，OE与抛物线的对称轴交于点E，连接AE、AD.求证：∠AEO＝∠ADC；  

    （3）以（2）中的点E为圆心，1为半径画圆，在对称轴右侧的抛物线上有一动点P，过点P作⊙O的切线，切点为Q，当PQ的长最小时，求点P的坐标.

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


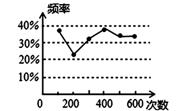
    甲、乙两名同学在一次用频率去估计概率的实验中，绘出了某一结果出现的频率的折线图，则符合这一结果的实验可能是

    A. 掷一枚正六面体的骰子，出现1点的概率

    B. 抛一枚硬币，出现正面的概率

    C. 任意写一个整数，它能被2整除的概率

    D. 从一个装有2个白球和1个红球的袋子中任取一球，取到红球的概率

                    (第5题)                            (第6题)

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某中学九年级一位同学不幸得了重病，牵动了全校师生的心，该校开展了“献爱心”捐款活动.第一天收到捐款10 000元，第三天收到捐款12 100元.

    (1) 如果第二天、第三天收到捐款的增长率相同，求捐款增长率；

    (2) 按照(1)中收到捐款的增长速度，第四天该校能收到多少捐款？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    因式分解：2m2－8m＋8＝_______．

    查看答案和解析>>

    同步练习册答案