
����Ŀ��ij�������쳧����һ����ʽ�綯�������ƻ�һ��������װ240�������ڳ�������㹻���������������ʽ�綯�����İ�װ������������ƸһЩ�¹��ˣ����Ǿ�����ѵ���ϸڣ�Ҳ�ܶ������е綯�����İ�װ��������ʼ���в��ŷ��֣�1����������2���¹���ÿ�¿ɰ�װ8���綯������2����������3���¹���ÿ�¿ɰ�װ14���綯������
��1��ÿ�����������¹���ÿ�·ֱ����װ�������綯������
��2�����������Ƹn��0<n<10�����¹��ˣ�ʹ����Ƹ���¹��˺ͳ�����������պ������һ��İ�װ������ô�������ļ����¹��˵���Ƹ������
��3���ڣ�2���������£���������װ�綯������ÿ��������ÿ�·�2000Ԫ�Ĺ��ʣ���ÿ���¹���ÿ�·�1200Ԫ�Ĺ��ʣ���ô����Ӧ��Ƹ�������¹��ˣ�ʹ�¹��˵�����������������ͬʱ����ÿ��֧���Ĺ����ܶ�W��Ԫ�������ܵ��٣�
���𰸡���1��ÿ��������ÿ�¿���װ4���綯�����¹���ÿ�·ֱ�װ2���綯����
��2����������1�ˣ��¹���8�ˣ���������2�ˣ��¹���6�ˣ���������3�ˣ��¹���4�ˣ���������4�ˣ��¹���2�ˣ�
��3��ѡ����
��������
��1����ÿ��������ÿ�¿���װx���綯�����¹���ÿ�·ֱ�װy���綯����
![]() ,��֮��
,��֮��![]() .
.
ÿ��������ÿ�¿���װ4���綯�����¹���ÿ�·ֱ�װ2���綯����
��2�����������m�ˣ��������![]() ��
��![]() ����Ϊ0<n<10, ��m=1,2,3,4ʱn=8,6,4,2
����Ϊ0<n<10, ��m=1,2,3,4ʱn=8,6,4,2
��������1�ˣ��¹���8�ˣ���������2�ˣ��¹���6�ˣ���������3�ˣ��¹���4�ˣ���������4�ˣ��¹���2�ˣ�
��3������һ:![]() ��������:
��������:![]() ��
��
������:![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC����ǡ�EAC��ƽ����AD�������Բ��O�ڵ�D������DB��DC��
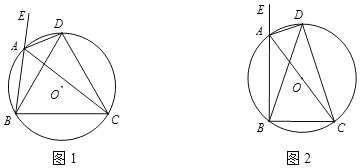
��1����ͼ1����֤BD��CD��
��2����ͼ2����AC�ǡ�O��ֱ����sin��BDC��![]() ����tan��DBA��ֵ��
����tan��DBA��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
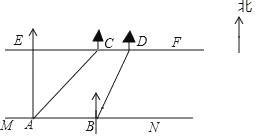
����Ŀ�������ʵ�����ϣ�С������С��Ҫ����һ��С�ӵĿ��ȣ���ͼ���Ӱ�EF��MN��С���ںӰ�MN�ϵĵ�A����úӶ�С��Cλ�ڶ�������Ȼ�����غӰ�����30�ף�����B����úӶ�С��Dλ�ڱ�ƫ��30��ķ�������ͬѧ���CD��10��
��1����EAC���� ���ȣ���DBN���� ���ȣ�
��2����С�ӵĿ���AE���������ȷ��0.1�ף��ο����ݣ�![]() ��1.414��
��1.414��![]() ��1.732��
��1.732��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
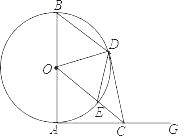
����Ŀ����ͼ��ABΪ��O��ֱ��������AGΪ��O�����ߣ���AΪ�е㣬��CΪ����AG������һ�㣬����OC����O�ڵ�E������B��BD��OC����O�ڵ�D������CD��DE��OD��
��1����֤����OAC�ա�ODC��
��2���ٵ���OCA�Ķ���Ϊ�� ��ʱ���ı���BOEDΪ���Σ�
�ڵ���OCA�Ķ���Ϊ�� ��ʱ���ı���OACDΪ�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC����������͵�O��������������ĸ���ϣ�ÿ��С�����εı߳���Ϊ1��
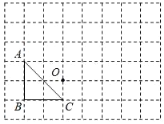
��1������ABC������ƽ��4����λ��������ƽ��2����λ�õ���A1B1C1���뻭����A1B1C1��
��2���뻭����A2B2C2��ʹ��A2B2C2����ABC���ڵ�O�����ĶԳƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a�����������ҹ���x��һԪ���η��̣�a��2��x2+4x+1��0��ʵ���⣮��aʹ����y�ķ�ʽ����![]() ��������ĸ���Ϊ_____��
��������ĸ���Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
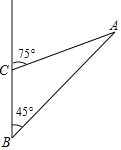
����Ŀ���ɶ��е�ʮ���ε��������ʵʩ��������ս�ԣ��ƶ��˳��з�չ�����ǧ��֮�����ɶ���Ȫɽ����ɭ�ֹ�����������֮�磬��ȫ��֮������������һ�������������ij������ģ���ͼΪ�ɶ�����Ȫɽ���к��ֹ���������A��B��C��ƽ��ʾ��ͼ������C��B����������5ǧ�״�������A��B�Ķ���������C�ı�ƫ��75�������ϣ�
��1����BAC�Ĵ�С
��2����A��C�ľ��루![]() ��1.414��
��1.414��![]() ��1.732��sin75���0.966��cos75���0.259��tan75���3.732�������ȷ��0.1��
��1.732��sin75���0.966��cos75���0.259��tan75���3.732�������ȷ��0.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪AM�ǡ�ABC�����ߣ���D���߶�AM��[��D�����A�غϣ�������D��DF��AB��AC���ڵ�F������C��CE��AM��DF���ӳ����ڵ�E������AE��
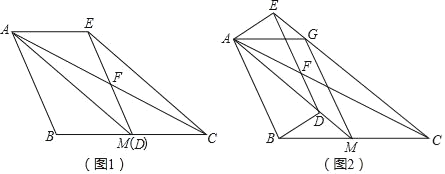
��1����ͼ1������D���M�غ�ʱ����֤���ı���ABDE��ƽ���ı��Σ�
��2����ͼ2������D�����M�غ�ʱ������M��MG��DE��EC�ڵ�G������BD��AG�ڲ������κθ����ߵ�����£���ֱ��д��ͼ�����е�ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AC��BC����ACB��90�㣬��D�ڱ�BC�ϣ�BD��6��CD��2����P�DZ�AB��һ�㣬��PC��PD����СֵΪ___.
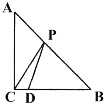
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com