
【题目】已知△ABC的外角∠EAC的平分线AD交其外接圆⊙O于点D,连接DB,DC.
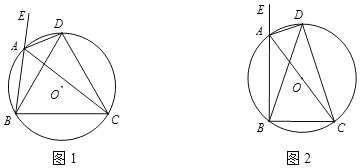
(1)如图1,求证BD=CD;
(2)如图2,若AC是⊙O的直径,sin∠BDC=![]() ,求tan∠DBA的值.
,求tan∠DBA的值.
【答案】(1)见解析;(2)tan∠DBA=![]() .
.
【解析】
(1)根据圆周角定理可证∠DAC=∠DBC,根据圆内接四边形的性质可证∠EAD=∠DCB,又已知∠EAD=∠DAC,即∠DCB=∠DBC得证,进而证明即可;
(2)如图2,连接DO并延长交BC于F,连接OB,根据圆周角定理得到∠ABC=90°,求得sin∠BAC=![]() ,设BC=3a,AC=5a,则AB=4a,推出OD是BC的垂直平分线,得到BF=CF=
,设BC=3a,AC=5a,则AB=4a,推出OD是BC的垂直平分线,得到BF=CF=![]() a,根据三角形中位线定理得到OF=
a,根据三角形中位线定理得到OF=![]() AB=2a,求得DF=DO+OF=
AB=2a,求得DF=DO+OF=![]() a+2a=
a+2a=![]() a,根据三角函数的定义即可得到结论.
a,根据三角函数的定义即可得到结论.
(1)∵AD是∠EAC的平分线,
∴∠EAD=∠DAC,
∵∠EAD是圆内接四边形ABCD的外角,
∴∠EAD=∠DCB(圆内接四边形外角等于内对角),
又∵∠DAC=∠DBC,
∴∠DCB=∠DBC,
∴DB=DC;
(2)如图2,连接DO并延长交BC于F,连接OB,
∵AC是⊙O的直径,
∴∠ABC=90°,
∵∠BDC=∠BAC,sin∠BDC=![]() ,
,
∴sin∠BAC=![]() ,
,
设BC=3a,AC=5a,则AB=4a,
∵OB=OC,BD=CD,
∴OD是BC的垂直平分线,
∴BF=CF=![]() a,
a,
∵AO=CO,
∴OF是△ABC斜边的中线,
∴BO=![]() a,
a,
∵AO=CO,
∴OF是△ABC的中位线,
∴OF=![]() AB=2a,
AB=2a,
∴DF=DO+OF=![]() a+2a=
a+2a=![]() a,
a,
∵∠DBA=∠ACD,OD=OC,
∴∠ACD=∠FDC,
∴∠DBA=∠FDC,
∴tan∠DBA=tan∠FDC=![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
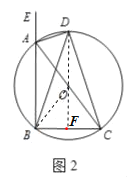
【题目】如图,抛物线y=ax2+5x+c交x轴于A,B两点,交y轴于点C,直线y=x﹣4经过点B,C.P是直线BC上方抛物线上一动点,直线PC交x轴于D.
(1)直接写出a,c的值;
(2)当△PBD的面积等于△BDC面积的一半时,求点P的坐标;
(3)当∠PBA=![]() ∠CBP时,直接写出直线BP的解析式.
∠CBP时,直接写出直线BP的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“食品安全真重要,病从口入危害大.良好习惯要养成,食品挑选切注意.”是食品卫生安全歌谣中的一段歌词,某中学针对一些学生不吃正餐,爱吃街边小吃及一些三无小食品,严重危害身体健康的情况,为提高学生们的食品安全意识组织了食品安全教育活动.学校就“是否会根据食品的三无情况来挑选日常食品”的问题在活动前随机抽取一部分学生进行调查,大致有以下五种观点:A:不吃“三无”食品;B:“三无”食品不太安全,可以少吃,但不能多吃;C:看着干净、卫生的食品就可以放心食用;D:高档的,贵的食品都可放心食用;E:不用关注食品的“三无”情况活动后再次调查这部分学生持这几种观点的情况,并将统计结果绘制成如下不完整的统计图(每位同学仅持一种观点).
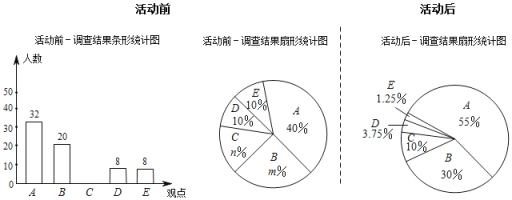
根据以上统计图,解答下列问题:
(1)活动前后,每次接受调查的学生总人数都为_____人,m=_____,n=_____;
(2)请补全活动前的调查结果条形统计图.
(3)若全校共有3200人,请你估计通过这次活动后,还有多少人持E种观点?
(4)根据活动前后的相关数据,说明活动的效果,并提出合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数![]() 的图象上,点C,D在反比例函数
的图象上,点C,D在反比例函数![]() 的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为( )
,则k的值为( )

A. 4 B. 3 C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
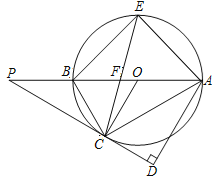
【题目】如图所示,AB是⊙O的直径,P为AB延长线上的一点,PC切⊙O于点C,AD⊥PC,垂足为D,弦CE平分∠ACB,交AB于点F,连接AE.
(1)求证:∠CAB=∠CAD;
(2)求证:PC=PF;
(3)若tan∠ABC=![]() ,AE=5
,AE=5![]() ,求线段PC的长.
,求线段PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点A,C落在坐标轴上,且顶点B的坐标为(﹣5,2),将△ABC沿x轴向右平移得到△A1B1C1,使得点B1恰好落在函数y=![]() 上,若线段AC扫过的面积为48,则点C1的坐标为( )
上,若线段AC扫过的面积为48,则点C1的坐标为( )
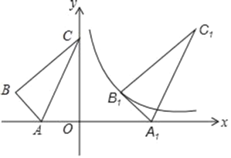
A.(3,2)B.(5,6)C.(8,6)D.(6,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,菱形ABCD中,直线l⊥边AB,并从点A出发向右平移,设直线l在菱形ABCD内部截得的线段EF的长为y,平移距离x=AF,y与x之间的函数关系的图象如图2所示,则菱形ABCD的面积为( )
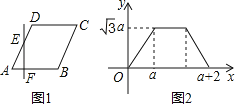
A.3B.![]() C.2
C.2![]() D.3
D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车制造厂开发一款新式电动汽车,计划一年生产安装240辆。由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人.他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘n(0<n<10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
(3)在(2)的条件下,工厂给安装电动汽车的每名熟练工每月发2000元的工资,给每名新工人每月发1200元的工资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时工厂每月支出的工资总额W(元)尽可能的少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com