
【题目】如图,在矩形OABC中,点A,B的坐标分别为A(4,0),B(4,3),动点N,P分别从点B,A同时出发,点N以1单位/秒的速度向终点C运动,点P以5/4单位/秒的速度向终点C运动,连结NP,设运动时间为t秒(0<t<4)
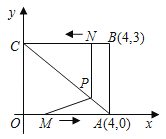
(1)直接写出OA,AB,AC的长度;
(2)求证:△CPN∽△CAB;
(3)在两点的运动过程中,若点M同时以1单位/秒的速度从点O向终点A运动,求△MPN的面积S与运动的时间t的函数关系式(三角形的面积不能为0),并直接写出当S=![]() 时,运动时间t的值.
时,运动时间t的值.
【答案】(1)OA=4,AB=3,AC=5;(2)见解析;(3)t的值为(3﹣![]() )秒
)秒
【解析】
(1)由矩形的性质和已知条件得出OA=BC=4,AB=OC=3,∠AOC=90°,由勾股定理求出AC=![]() =5;
=5;
(2)由题意得BN=t,AP=![]() t,证出
t,证出![]() =
=![]() ,得出PN∥AB,即可得出△CPN∽△CAB;
,得出PN∥AB,即可得出△CPN∽△CAB;
(3)①当0<t<2时,延长NP交OA于D,由相似三角形的性质得![]() =
=![]() =
=![]() ,求出PD=
,求出PD=![]() t,AD=t,得出PN=3﹣
t,AD=t,得出PN=3﹣![]() t,DM=4﹣2t,由三角形面积公式即可得出答案;
t,DM=4﹣2t,由三角形面积公式即可得出答案;
②2<t<4时,延长NP交OA于D,由相似三角形的性质得出![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,求出PD=
,求出PD=![]() t,AD=t,得出PN=3﹣
t,AD=t,得出PN=3﹣![]() t,DM=2t﹣4,由三角形面积公式即可得出答案;再把S=
t,DM=2t﹣4,由三角形面积公式即可得出答案;再把S=![]() 分别代入两个关系式,解方程即可.
分别代入两个关系式,解方程即可.
(1)证明:∵四边形OABC是矩形,A(4,0),B(4,3),
∴OA=BC=4,AB=OC=3,∠AOC=90°,
∴AC=![]() =
=![]() =5;
=5;
(2)解:由题意得:BN=t,AP=![]() t,
t,
∵![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴PN∥AB,
∴△CPN∽△CAB;
(3)解:分两种情况:
①当0<t<2时,延长NP交OA于D,如图1所示:
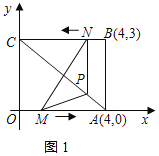
由(2)得:PD∥AB,
∴△APD∽△ACO,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
解得:PD=![]() t,AD=t,
t,AD=t,
∴PN=3﹣![]() t,DM=4﹣t﹣t=4﹣2t,
t,DM=4﹣t﹣t=4﹣2t,
∴△MPN的面积S=![]() PN×DM=
PN×DM=![]() ×(3﹣
×(3﹣![]() t)×(4﹣2t)=
t)×(4﹣2t)=![]() t2﹣
t2﹣![]() t+6,
t+6,
即S=![]() t2﹣
t2﹣![]() t+6(0<t<2);
t+6(0<t<2);
②当2<t<4时,延长NP交OA于D,如图2所示:
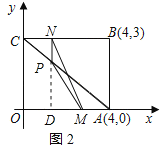
由(2)得:PD∥AB,
∴△APD∽△ACO,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
解得:PD=![]() t,AD=t,
t,AD=t,
∴PN=3﹣![]() t,DM=t+﹣4t=2t﹣4,
t,DM=t+﹣4t=2t﹣4,
∴△MPN的面积S=![]() PN×DM=
PN×DM=![]() ×(3﹣
×(3﹣![]() t)×(2t﹣4)=﹣
t)×(2t﹣4)=﹣![]() t2+
t2+![]() t﹣6,
t﹣6,
即S=﹣![]() t2+
t2+![]() t﹣6(2<t<4);
t﹣6(2<t<4);
当S=![]() ,0<t<2时,则
,0<t<2时,则![]() t2﹣
t2﹣![]() t+6=
t+6=![]() ,
,
整理得:t2﹣6t+6=0,
解得:t=3﹣![]() ,或t=3+
,或t=3+![]() (不合题意舍去),
(不合题意舍去),
∴t=3﹣![]() ;
;
当S=![]() ,2<t<4时,则﹣
,2<t<4时,则﹣![]() t2+
t2+![]() t﹣6=
t﹣6=![]() ,
,
整理得:t2﹣6t+10=0,
∵△=36﹣40<0,
∴此方程无解;
综上所述,当S=![]() 时,运动时间t的值为(3﹣
时,运动时间t的值为(3﹣![]() )秒.
)秒.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】一个四位数,记千位上和百位上的数字之和为![]() ,十位上和个位上的数字之和为
,十位上和个位上的数字之和为![]() ,如果
,如果![]() ,那么称这个四位数为“和平数”.例如:1423,
,那么称这个四位数为“和平数”.例如:1423,![]() ,
,![]() ,因为
,因为![]() ,所以1423是“和平数”.
,所以1423是“和平数”.
(1)直接写出:最小的“和平数”是_________________,最大的“和平数”是_______________;
(2)求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是12的倍数的所有“和平数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】奇思参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题奇思都不会,不过奇思还有两个“求助”可以使用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果奇思两次“求助”都在第一道单选题中使用,求他通关的概率;
(2)如果奇思每道单选题各使用一次“求助",请用列表法或画树状图的方法求他顺利通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D在圆上,![]() =
=![]() ,过点C作CE⊥AD延长线于点E.
,过点C作CE⊥AD延长线于点E.
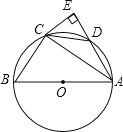
(1)求证:CE是⊙O的切线;
(2)若BC=3,AC=4,求CE和AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图像经过点
的图像经过点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,二次函数
,二次函数![]() 的图像经过点
的图像经过点![]() 和点
和点![]() ,顶点为
,顶点为![]() ,对称轴与一次函数的图像相交于点
,对称轴与一次函数的图像相交于点![]() 。
。
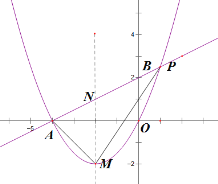
(1)求一次函数的解析式以及![]() 点,
点,![]() 点的坐标;
点的坐标;
(2)求顶点![]() 的坐标;
的坐标;
(3)在![]() 轴上求一点
轴上求一点![]() ,使得
,使得![]() 和
和![]() 相似。
相似。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016·宁夏中考)如图,已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2![]() ,求CD的长.
,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
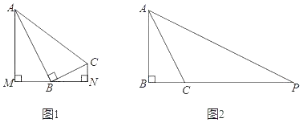
【题目】在∠ABC中,∠ABC=90°,tan∠BAC=![]() .
.
(1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,若点B恰好是线段MN的中点,求tan∠BAM的值;
(2)如图2,P是边BC延长线上一点,∠APB=∠BAC,求tan∠PAC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac;②2a+b=0;③a﹣b+c=0;④5a<b.其中正确的有( )
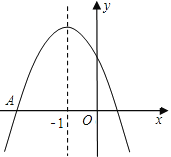
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com