
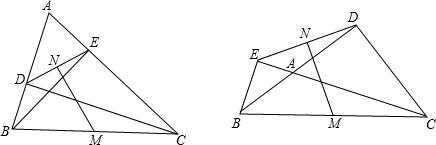
如图,△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点.
(1)求证:MN⊥DE;
(2)连结DM,ME,猜想∠A与∠DME之间的关系,并写出推理过程;
(3)若将锐角△ABC变为钝角△ABC,如图,上述(1)(2)中的结论是否都成立?若结论成立,直接回答,不需证明;若结论不成立,说明理由.
【考点】直角三 角形斜边上的中线;
角形斜边上的中线; 等腰三角形的判定与性质.
等腰三角形的判定与性质.
【分析】(1)连接DM、ME,根据直角三角形斜边上的中线等于斜边的一半可得DM=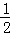 BC,ME=
BC,ME=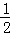 BC,从而得到DM=ME,再根据等腰三角形三线合一的性质证明;
BC,从而得到DM=ME,再根据等腰三角形三线合一的性质证明;
(2)根据三角形的内角和定理可得∠ABC+∠ACB=180°﹣∠A,再根据等腰三角形两底角相等表示出∠BMD+∠CME,然后根据平角等于180°表示出∠DME,整理即可得解;
(3)根据三角形的内角和定理可得∠ABC+∠ACB=180°﹣∠A,再根据等腰三角形两底角相等和三角形的一个外角等于与它不相邻的两个内角的和表示出∠BME+∠CME,然后根据平角等于180°表示出∠DME,整理即可得解.
【解答】解:(1)如图,连接DM,ME,
∵CD、BE分别是AB、AC边上的高,M是BC的中点,
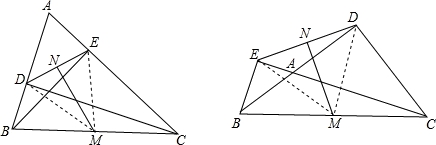
∴DM=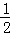 BC,ME=
BC,ME=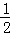 BC,
BC,
∴DM=ME
又∵N为DE中点,
∴MN⊥DE;
(2)在△ABC中,∠ABC+∠ACB=180°﹣∠A,
∵DM=ME=BM=MC,
∴∠BMD+∠CME=(180°﹣2∠ABC)+(180°﹣2∠ACB),
=360°﹣2(∠ABC+∠ACB),
=360°﹣2(180°﹣∠A),
=2∠A,
∴∠DME=180°﹣2∠A;
(3)结论(1)成立,
结论(2)不成立,
理由如下:在△ABC中,∠ABC+∠ACB=180°﹣∠A,
∵DM=ME=BM=MC,
∴∠BME+∠CMD=2∠ACB+2∠ABC,
=2(180°﹣∠A),
=360°﹣2∠A,
∴∠DME=180°﹣(360°﹣2∠A),
=2∠A﹣180°.
【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形两底角相等的性质,三角形的内角和定理,整体思想的利用是解题的关键.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
按照要求完成下列各题:
(1)如图1,在平面直角坐标系中,线段AB的两个端点是A(﹣5 ,1),B(﹣2,3).
,1),B(﹣2,3).
①写出与线段AB的两个端点关于x轴对称的两个点C、D的坐标;
②在此坐标系中画出线段CD.
(2)如图2,已知线段a、b、c,∠β.
求作:△ABC,使BC=a,AB=b,∠B=∠β.(要求:不写作法,保留作图痕迹,写出作图结论)

查看答案和解析>>
科目:初中数学 来源: 题型:
观察下列算式:a=﹣|﹣3|,b=+(﹣0.5),c=|﹣4|﹣|﹣5|,则a,b,c的大小关系是( )
A.b>c>a B.a>c>b C.a>b>c D.c>b>a
查看答案和解析>>
科目:初中数学 来源: 题型:
有这样一道计算题:3x2y+[2x2y﹣(5x2y2﹣2y2)]﹣5(x2y+y2﹣x2y2)的值,其中x=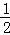 ,y=﹣1.小明同学把“x=
,y=﹣1.小明同学把“x=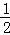 ”错看成“x=﹣
”错看成“x=﹣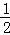 ”,但计算结果仍正确;小华同学把“y=﹣1”错看成“y=1”,计算结果也是正确的,你知道其中的道理吗?请加以说明.
”,但计算结果仍正确;小华同学把“y=﹣1”错看成“y=1”,计算结果也是正确的,你知道其中的道理吗?请加以说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com