
【题目】定义:在平面直角坐标系xOy中,把从点P出发沿纵或横方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若P(﹣1,1),Q(2,3),则P,Q的“实际距离”为5,即PS+SQ=5或PT+TQ=5.环保低碳的共享单车,正式成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为A(3,1),B(5,﹣3),C(﹣1,﹣5),若点M表示单车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标为( )
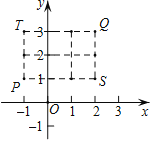
A. (1,﹣2)B. (2,﹣1)C. (![]() ,﹣1)D. (3.0)
,﹣1)D. (3.0)
【答案】A
【解析】
若设M(x,y),构建方程组即可解决问题.
设M(x,y),由“实际距离”的定义可知:
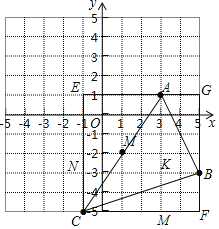
点M只能在ECFG区域内,
﹣1<x<5,﹣5<y<1,
又∵M到A,B,C距离相等,
∴|x﹣3|+|y﹣1|=|x﹣5|+|y+3|=|x+1|+|y+5|,①
∴|x﹣3|+1﹣y=5﹣x+|y+3|=x+1+y+5,②
要将|x﹣3|与|y+3|中绝对值去掉,
需要判断x在3的左侧和右侧,以及y在﹣3的上侧还是下侧,
将矩形ECFG分割为4部分,若要使M到A,B,C的距离相等,
由图可知M只能在矩形AENK中,
故x<3,y>﹣3,
则方程可变为:3﹣x+1﹣y=y+5+x+1=5﹣x+3+y,
解得,x=1,y=﹣2,则M(1,﹣2)
故选:A.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() (
(![]() )与
)与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),与
左侧),与![]() 轴交于点
轴交于点![]() ,该抛物线的顶点
,该抛物线的顶点![]() 的纵坐标是
的纵坐标是![]() .
.

(1)求点![]() 、
、![]() 的坐标;
的坐标;
(2)设直线与直线![]() 关于该抛物线的对称轴对称,求直线的表达式;
关于该抛物线的对称轴对称,求直线的表达式;
(3)平行于![]() 轴的直线
轴的直线![]() 与抛物线交于点
与抛物线交于点![]() 、
、![]() ,与直线交于点
,与直线交于点![]() .若
.若![]() ,结合函数图象,求
,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
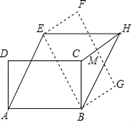
【题目】如图,矩形ABCD中,AB=3,AD=![]() ,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM=( )
,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM=( )
A. ![]() B. 1 C.
B. 1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了科学建设“学生健康成长工程”.随机抽取了部分学生家庭对其家长进行了主题为“周末孩子在家您关心吗?”的问卷调查,将回收的问卷进行分析整理,得到了如下的样本统计表和扇形统计图:
代号 | 情况分类 | 家庭数 |
| 带孩子玩并且关心其作业完成情况 | 16 |
| 只关心其作业完成情况 | b |
| 只带孩子玩 | 8 |
| 既不带孩子玩也不关心其作业完成情况 | d |
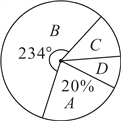
(1)求![]() 的值;
的值;
(2)该校学生家庭总数为500,学校决定按比例在![]() 类家庭中抽取家长组成培训班,其比例为
类家庭中抽取家长组成培训班,其比例为![]() 类取20%,
类取20%,![]() 类各取60%,请你估计该培训班的家庭数;
类各取60%,请你估计该培训班的家庭数;
(3)若在![]() 类家庭中只有一个城镇家庭,其余是农村家庭,请用列举法求出在
类家庭中只有一个城镇家庭,其余是农村家庭,请用列举法求出在![]() 类中随机抽出2个家庭进行深度采访,其中有一个是城镇家庭的概率.
类中随机抽出2个家庭进行深度采访,其中有一个是城镇家庭的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,![]() ≈1.4)
≈1.4)

查看答案和解析>>
科目:初中数学 来源: 题型:
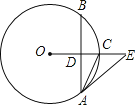
【题目】如图,在⊙O中,半径OC垂直于弦AB,垂足为点D,点E在OC的延长线上,∠EAC=∠BAC
(1)求证:AE是⊙O的切线;
(2)若AB=8,cosE=![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,AB=4,点F,C是⊙O上两点,连接AC,AF,OC,弦AC平分∠FAB,∠BOC=60°,过点C作CD⊥AF交AF的延长线于点D,垂足为点D.
(1)求扇形OBC的面积(结果保留π);
(2)求证:CD是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2011年高中招生考试,某中学对全校九年级学生进行了一次数学摸底考试,并随机抽取了部分学生的测试成绩作为样本进行,绘制成了如下两幅不完整的统计图,请根据图中所给信息,下列问题:
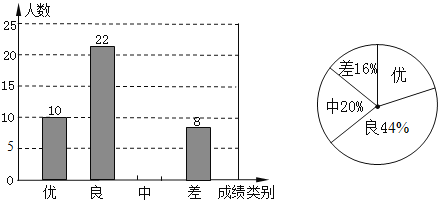
(1)请将表示成绩类别为“中”的条形统计图补充完整;
(2)在扇形统计图中,表示成绩类别为“优”的扇形所对应的圆心角是 72 度;
(3)学校九年级共有1000人参加了这次数学考试,估算该校九年级共有多少名学生的数学成绩可以达到优秀?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com