
如图,▱ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=
 ,则AB的长是 .
,则AB的长是 .


1 .
【考点】平行四边形的判定与性质;含30度角的直角三角形;勾股定理.
【分析】根据平行四边形性质推出AB=CD,AB∥CD,得出平行四边形ABDE,推出DE=DC=AB,根据直角三角形性质求出CE长,即可求出AB的长.
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=CD,
∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE=CD,
即D为CE中点,
∵EF⊥BC,
∴∠EFC=90°,
∵AB∥CD,
∴∠DCF=∠ABC=60°,
∴∠CEF=30°,
∵EF=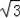
 ,
,
∴CE=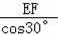
 =2,
=2,
∴AB=1,
故答案为:1.
【点评】本题考查了平行四边形的性质和判定,平行线性质,勾股定理,直角三角形斜边上中线性质,含30度角的直角三角形性质等知识点的应用,此题综合性比较强,是一道比较好的题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
已知关于x的一元二次方程(a﹣1)x2﹣2x+1=0有两个不相等的实数根,则a的取值范围是( )
A.a>2 B.a<2 C.a<2且a≠l D.a<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
已知直线y=kx﹣3与x轴交于点A (4,0),与y轴交于点C.抛物线y=﹣
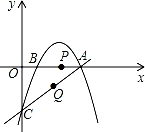
(4,0),与y轴交于点C.抛物线y=﹣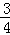 x2+mx+n经过点A和点C.且与x轴交于点B,动点P在x轴上以每秒1个单位长度的速度由点B向点A运动.点Q由点C沿线段CA向点A运动.且速度是点P运动速度的2倍.
x2+mx+n经过点A和点C.且与x轴交于点B,动点P在x轴上以每秒1个单位长度的速度由点B向点A运动.点Q由点C沿线段CA向点A运动.且速度是点P运动速度的2倍.
(1)求直线的解析式和抛物线的解析式;
(2)如果点P和点Q同时出发.运动时间为t(秒).试问当t为何值时,以A、P、Q为顶点的三角形与△AOC相 似.
似.
查看答案和解析>>
科目:初中数学 来源: 题型:
种植能手李大叔种植了一批新品种黄瓜,为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到如图的条形图,则抽查的这部分黄瓜株上所结黄瓜根数的中位数和众数分别是( )
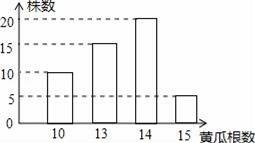

A.13.5,20 B.15,5 C.13.5,14 D.13,14
查看答案和解析>>
科目:初中数学 来源: 题型:
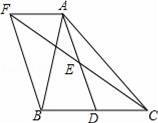
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
(3)在(2)的条件下,△ABC满足条件 ,矩形AFBD是正方形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com