
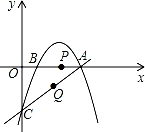
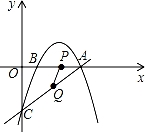
已知直线y=kx﹣3与x轴交于点A (4,0),与y轴交于点C.抛物线y=﹣
(4,0),与y轴交于点C.抛物线y=﹣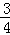 x2+mx+n经过点A和点C.且与x轴交于点B,动点P在x轴上以每秒1个单位长度的速度由点B向点A运动.点Q由点C沿线段CA向点A运动.且速度是点P运动速度的2倍.
x2+mx+n经过点A和点C.且与x轴交于点B,动点P在x轴上以每秒1个单位长度的速度由点B向点A运动.点Q由点C沿线段CA向点A运动.且速度是点P运动速度的2倍.
(1)求直线的解析式和抛物线的解析式;
(2)如果点P和点Q同时出发.运动时间为t(秒).试问当t为何值时,以A、P、Q为顶点的三角形与△AOC相 似.
似.
【考点】二次函数综合题.
【专题】综合题.
【分析】(1)先把A点坐标代入y=kx﹣3可求出k得到直线的解析式为y=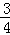 x﹣3,再利用直线解析式求出C(0
x﹣3,再利用直线解析式求出C(0 ,﹣3),然后利用待定系数法求抛物线的解析式;
,﹣3),然后利用待定系数法求抛物线的解析式;
(2)利用抛物线与x轴的交点问题求出B(1,0),则可根据勾股定理计算出AB=5,则AP=3﹣t,AQ=5﹣2t,然后分类讨论:由于∠PAQ=∠OAC,所以当∠APQ=∠AOC时,△APQ∽△AOC, 利用相似比得到
利用相似比得到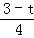 =
=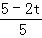 ;当∠APQ=∠AOC时,△APQ∽△ACO,利用相似比得到
;当∠APQ=∠AOC时,△APQ∽△ACO,利用相似比得到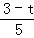 =
= ,再分别解关于t的方程求出t即可.
,再分别解关于t的方程求出t即可.
【解答】解:(1)把A(4,0)代入y=kx﹣3得4k﹣3=0,解得k=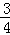 ,则直线的解析式为y=
,则直线的解析式为y=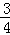 x﹣3;
x﹣3;
当x=0时,y=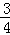 x﹣3=﹣3,则C(0,﹣3),
x﹣3=﹣3,则C(0,﹣3),
把A(4,0),C(0,﹣3)代入y=﹣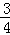 x2+mx+n得
x2+mx+n得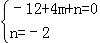 ,解得
,解得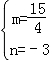 .
.
所以抛物线的解析式为y=﹣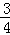 x2+
x2+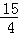 x﹣3;
x﹣3;
(2)对于抛物线y=﹣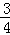 x2+
x2+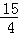 x﹣3;
x﹣3;
当y=0,﹣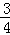 x2+
x2+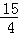 x﹣3=0,解得x1=1,x2=4,
x﹣3=0,解得x1=1,x2=4,
∴B(1,0),
∴AB=3,
∵AO=4,
∴AC=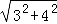 =5,
=5,
∴AP=3﹣t,AQ=5﹣2t,
∵∠PAQ=∠OAC,
∴当∠APQ=∠AOC时,△APQ∽△AOC,则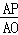 =
=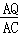 ,即
,即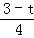 =
=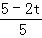 ,解得t=
,解得t=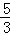 ;
;
当∠APQ=∠AOC时,△APQ∽△ACO,则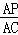 =
=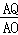 ,即
,即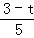 =
= ,解得t=
,解得t=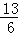 ,
,
综上所述,当t的值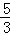
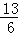 时,以P、Q、A为顶点的三角形与△AOC相似.
时,以P、Q、A为顶点的三角形与△AOC相似.
【点评】本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和一次函数图象上点的坐标特征;能用待定系数法求函数解析式,会求抛物线与x轴的交点坐标;灵活运用相似三角形的判定与性质和分类讨论思想.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
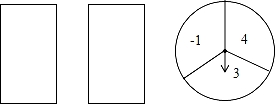
小云玩抽卡片和旋转盘游戏,有两张正面分别标有数字1,2的不透明卡片,背面完全相同;转盘被平均分成3个相等的扇形,并分别标有数字﹣1,3,4(如图所示),小云把卡片背面朝上洗匀后从中随机抽出一张,记下卡片上的数字;然后转动转盘,转盘停止后,记下指针所在区域的数字(若指针在分格线上,则重转一次,直到指针指向某一区域为止).
(1)请用列表或树状图的方法(只选其中一种),表示出两次所得数字可能出现的所有结果;
(2)求出两个数字之积为负数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
不透明的口袋里装有红、黄、蓝三种颜色的小球若干个(除颜色外其余都相同),其中红球2个(分别标有1号、2号),蓝球1个.若从中任意摸出一个球,它是蓝球的概率为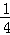 .
.
(1)求袋中黄球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用画树状图或列表格的方法,求两次摸到不同颜色球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
兴义市进行城区规划,工程师需测某楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进30m到达E,又测得楼顶端A的仰角为60°,楼AB的高为( )


A.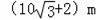
 B.
B.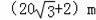
 C.
C.
 D.
D.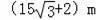

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,ABC的顶点的坐标分别为A(﹣1,5)、B(﹣1,1)、C(﹣3,1).将△ABC向右平移2个单位、再向下平移4个单位得到△A1B1C1;将△ABC绕原点O旋转180°得到△A2B2C2
(1)请直接写出点C1和C2的坐标;
(2)请直接写出线段A1A2的长;
(3)请直接写出将△ABC绕直线AB旋转一周所得的立体图形的表面积.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com