
不透明的口袋里装有红、黄、蓝三种颜色的小球若干个(除颜色外其余都相同),其中红球2个(分别标有1号、2号),蓝球1个.若从中任意摸出一个球,它是蓝球的概率为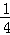 .
.
(1)求袋中黄球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用画树状图或列表格的方法,求两次摸到不同颜色球的概率.
【考点】列表法与树状图法;概率公式.
【分析】(1)利用概率的求解方法,借助于方程求解即可;
(2)此题需要两步完成,所以采用树状图法或者采用列表法都比较简单;解题时要注意是放回实验还是不放回实验,此题属于不放回实验.
【解答】解:(1)设袋中黄球的个数为x个,
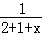 =
=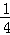
∴x=1
∴袋中黄球的个数为 1个;(
1个;( 2分)
2分)
(2)方法一、列表如下:(6分)
| * | 红1 | 红2 | 黄 | 蓝 |
| 红1 | * | (红1,红2) | (红1,黄) | (红1,蓝) |
| 红2 | (红2,红1) | * | (红2,黄) | (红2,蓝) |
| 黄 | (黄,红1) | (黄,红2) | * | (黄,蓝) |
| 蓝 | (蓝,红1) | (蓝,红2) | (蓝,黄) | * |
∴一共有12种情况,两次摸到不同颜色球的有10种情况,
∴两次摸到不同颜色球的概率为: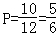 .(8分)
.(8分)
方法二,画树状图如下:
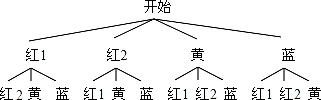
【点评】(1)注意利用方程思想,掌握概率公式的求法;
(2)此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:
关于x的方程﹣x2+2(k﹣1)x﹣k2+1=0有两个不相等的实数根.
(1)求k的取值范围;
(2)当k为何值时,方程的两个实数根的平方和等于16?
查看答案和解析>>
科目:初中数学 来源: 题型:
已知关于x的一元二次方程(a﹣1)x2﹣2x+1=0有两个不相等的实数根,则a的取值范围是( )
A.a>2 B.a<2 C.a<2且a≠l D.a<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
已知直线y=kx﹣3与x轴交于点A (4,0),与y轴交于点C.抛物线y=﹣
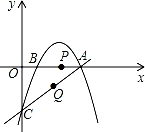
(4,0),与y轴交于点C.抛物线y=﹣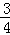 x2+mx+n经过点A和点C.且与x轴交于点B,动点P在x轴上以每秒1个单位长度的速度由点B向点A运动.点Q由点C沿线段CA向点A运动.且速度是点P运动速度的2倍.
x2+mx+n经过点A和点C.且与x轴交于点B,动点P在x轴上以每秒1个单位长度的速度由点B向点A运动.点Q由点C沿线段CA向点A运动.且速度是点P运动速度的2倍.
(1)求直线的解析式和抛物线的解析式;
(2)如果点P和点Q同时出发.运动时间为t(秒).试问当t为何值时,以A、P、Q为顶点的三角形与△AOC相 似.
似.
查看答案和解析>>
科目:初中数学 来源: 题型:
种植能手李大叔种植了一批新品种黄瓜,为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到如图的条形图,则抽查的这部分黄瓜株上所结黄瓜根数的中位数和众数分别是( )
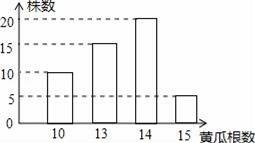

A.13.5,20 B.15,5 C.13.5,14 D.13,14
查看答案和解析>>
科目:初中数学 来源: 题型:
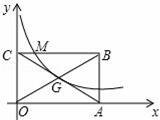
如图,矩形OABC的两点OA、OC分别在x轴、y轴的正半轴上,点G为矩形对角线的交点,经过点G的双曲线y=
 在第一象限的图象与BC相交于点M,交AB于N,若已知S△MBN=9,则k的值为 .
在第一象限的图象与BC相交于点M,交AB于N,若已知S△MBN=9,则k的值为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com