
关于x的方程﹣x2+2(k﹣1)x﹣k2+1=0有两个不相等的实数根.
(1)求k的取值范围;
(2)当k为何值时,方程的两个实数根的平方和等于16?
【考点】根的判别式;根与系数的关系.
【分析】(1)由于关于x的方程﹣x2+2(k﹣1)x﹣k2+1=0有两个不相等的实数根,根据方程的判别式大于0,由此即可确定k的取值范围;
(2)首先根据一元二次方程根与系数的关系得到两根之和与两根之积,然后把两个实数根的平方和变换两根之和与两根之积相关的形式,由此即可得到关于k的方程,解方程就可以求出k的值.
【解答】解:(1)由题意得,△=(2(k﹣1))2﹣4(k2﹣1)=﹣8k+8>0,
解得,k<1,
故k的取值范围:k<1;
(2)设方程的两根为x1,x2,
由x12+x22=( x1+x2)2﹣2 x1x2=(2(k﹣1))2﹣2(k2﹣1)=2k2﹣8k+6=16,
解得,k=﹣1或5(舍去),
当k=﹣1时,方程的两个实数根的平方和等于16.
【点评】此题考查了一元二次方程根的情况与判别式△的关系和一元二次方程根与系数的关系,综合性比较强.第一小题通过利用一元二次方程根的情况与判别式△的关系得到关于k的不等式解决问题;第二小题通过利用一元二次方程根与系数的关系得到关于k的方程解决问题.


 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
如图,∠BOC=10°,点A在OB上,且OA=1,按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n= .

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,矩形ABCD中,AB=3,AD=4,动点E从B点沿BC边移动到C停止,DF⊥AE于F,设E在运动过程中,AE长为x,DF长为y,则下列能反映y与x函数关系的是( )


A.y=7x B.y=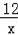
 C.y=
C.y=
 D.y=
D.y=

查看答案和解析>>
科目:初中数学 来源: 题型:
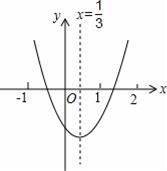
小明从图示的二次函数y=ax2+bx+c的图象中,观察得出了下面4条信息:
①abc>0;②a﹣b+c>0;③2a﹣3b=0;④c﹣4b>0.你认为其中正确信息是 (填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
人的眼睛可以看见的红光的波长是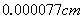 ,用科学记数法表示为( )cm.
,用科学记数法表示为( )cm.
A. 0.77×10-6 B. 77×10- 4 C. 7.7×10-5 D. 7.7×10-6
4 C. 7.7×10-5 D. 7.7×10-6
查看答案和解析>>
科目:初中数学 来源: 题型:
不透明的口袋里装有红、黄、蓝三种颜色的小球若干个(除颜色外其余都相同),其中红球2个(分别标有1号、2号),蓝球1个.若从中任意摸出一个球,它是蓝球的概率为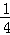 .
.
(1)求袋中黄球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用画树状图或列表格的方法,求两次摸到不同颜色球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com