
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=2.点P从点A出发,以每秒![]() 个单位长度的速度向终点C运动,点Q从点B出发,以每秒2个单位长度的速度向终点A运动,连接PQ,将线段PQ绕点Q顺时针旋转90°得到线段QE,以PQ、QE为边作正方形PQEF.设点P运动的时间为t秒(t>0)
个单位长度的速度向终点C运动,点Q从点B出发,以每秒2个单位长度的速度向终点A运动,连接PQ,将线段PQ绕点Q顺时针旋转90°得到线段QE,以PQ、QE为边作正方形PQEF.设点P运动的时间为t秒(t>0)
(1)点P到边AB的距离为______(用含t的代数式表示)
(2)当PQ∥BC时,求t的值
(3)连接BE,设△BEQ的面积为S,求S与t之间的函数关系式
(4)当E、F两点中只有一个点在△ABC的内部时,直接写出t的取值范围

【答案】(1)t;(2)t=1;(3)S=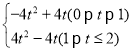 ;(4)详见解析.
;(4)详见解析.
【解析】
(1)作PH⊥AB交AB于点H,根据相似三角形,求出PH即可;
(2)根据平行线成比例性质,当PQ∥BC时,![]() ,即可求出t;
,即可求出t;
(3)分为0<t<1和1≤t≤2两种情况,进行讨论;
(4)根据题目,当F点在AB上时,此时t=1,当0<t≤1.时,当E、F至少有一个点在△ABC的内部,当1<t≤2时,没有点在内部.
解:(1)如图1,作PH⊥AB交AB于点H,
在Rt△ABC中,∠ABC=90°,AB=4,BC=2,AC=![]() .
.
根据题意,AP=![]() t,
t,
∵∠A=∠A,∠B=∠AHP,
∴△AHP~△ABC,
∴![]() ,即
,即![]() ,解得PH=t,
,解得PH=t,
即点P到边AB的距离为t.
故答案为t
(2)根据题意,AP=![]() ,BQ=2t,AQ=4-2t,
,BQ=2t,AQ=4-2t,
当PQ∥BC时,![]() ,即
,即![]() ,解得t=1
,解得t=1
(3)由(1)可知,E,F运动过程可分为两个阶段
当0<t<1,如图2,连接BE,作PH⊥AB交AB于点H,作GE⊥AB交AB于点G,
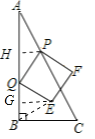
∵∠HPG+∠PQH=∠HQP+∠GQE=90°,
∵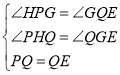 ,
,
∴△PHQ≌△QGE(AAS),
∴AH=BQ=2t,HQ=GE=4-4t,
S=![]() ,
,
当1≤t≤2,
连接BE,作PH⊥AB交AB于点H,作GE⊥AB交AB于点G,
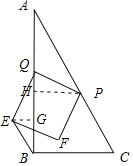
同理可证∴△PHQ≌△QGE(AAS),
∴AH=BQ=2t,HQ=GE=4t-4,
S=![]() ,
,
∵S>0,∴t≠0,
∴S=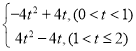 ;
;
(4)由(1)知,当F点在AB上时,此时t=1,
当0<t≤1.时,当E、F至少有一个点在△ABC的内部;当1<t≤2时,没有点在内部.


科目:初中数学 来源: 题型:
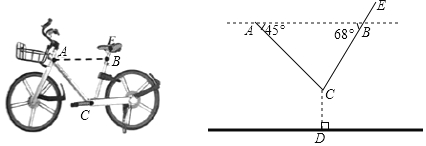
【题目】如图所示,一辆单车放在水平的地面上,车把头下方![]() 处与坐垫下方
处与坐垫下方![]() 处在平行于地面的同一水平线上,
处在平行于地面的同一水平线上,![]() ,
,![]() 之间的距离约为
之间的距离约为![]() ,现测得
,现测得![]() ,
,![]() 与
与![]() 的夹角分别为
的夹角分别为![]() 与
与![]() ,若点
,若点![]() 到地面的距离
到地面的距离![]() 为
为![]() ,坐垫中轴
,坐垫中轴![]() 处与点
处与点![]() 的距离
的距离![]() 为
为![]() ,求点
,求点![]() 到地面的距离(结果保留一位小数).(参考数据:
到地面的距离(结果保留一位小数).(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )

A. 2 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
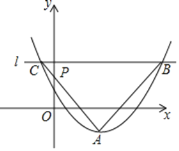
【题目】如图,在平面直角坐标系中,抛物线y=![]() -1的顶点为A,直线l过点P(0,m)且平行于x轴,与抛物线交于点B和点C.若AB=AC,∠BAC=90°,则m=______.
-1的顶点为A,直线l过点P(0,m)且平行于x轴,与抛物线交于点B和点C.若AB=AC,∠BAC=90°,则m=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
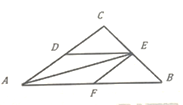
【题目】如图,在△ABC中,AB=3+![]() ,∠B=45°,∠C=105°,点 D、E、F分别在AC、BC、AB上,且四边形ADEF为菱形,若点P是AE上一个动点,则PF+PB的最小值为___________ 。
,∠B=45°,∠C=105°,点 D、E、F分别在AC、BC、AB上,且四边形ADEF为菱形,若点P是AE上一个动点,则PF+PB的最小值为___________ 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,BD为对角线.
(1)尺规作图:作CD边的垂直平分线EF,交CD于点E,交BD于点F(保留作图痕迹,不要求写作法);
(2)在(1)的条件下,若AB=4,求△DEF的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com