
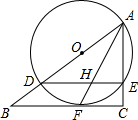
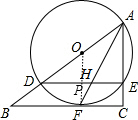
 如图,在Rt△ABC中,∠C=90°,点D是AB上一点,以AD为直径作⊙O交AC于E,与BC相切于点F,连接AF.
如图,在Rt△ABC中,∠C=90°,点D是AB上一点,以AD为直径作⊙O交AC于E,与BC相切于点F,连接AF.| 15 |
| 4 |
| 5 |
| 2 |
| 3 |
| 2 |
| CF |
| CB |
| AO |
| AB |
| 5 |
| FH |
| FA |
| CE |
| CA |
3
| ||
| 2 |
| AC2+BC2 |
| OF |
| AC |
| BO |
| BA |
| r |
| 6 |
| 10-r |
| 10 |
| 15 |
| 4 |
| 15 |
| 4 |
| 5 |
| 2 |
| BD |
| BA |
| CE |
| CA |
| ||
| 10 |
| CE |
| 6 |
| 3 |
| 2 |
| CF |
| CB |
| AO |
| AB |
| CF |
| 8 |
| ||
| 10 |
| AC2+CF2 |
| 5 |
| FH |
| FA |
| CE |
| CA |
| FH | ||
3
|
| 3 |
| 6 |
3
| ||
| 2 |
3
| ||
| 2 |
| 5 |
| 45 |
| 2 |


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
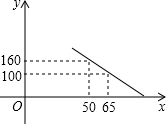 大学生王强积极响应“自主创业”的号召,准备投资销售一种进价为每件40元的小家电.通过试销发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.求y与x的函数表达式.
大学生王强积极响应“自主创业”的号召,准备投资销售一种进价为每件40元的小家电.通过试销发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.求y与x的函数表达式.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知Rt△ABC中,BC=9,AB=12,过点A作AE⊥AB,且AE=16,连接BE交AC于点P.
如图,已知Rt△ABC中,BC=9,AB=12,过点A作AE⊥AB,且AE=16,连接BE交AC于点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com