
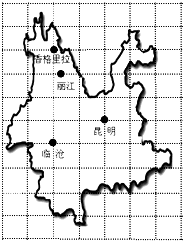
 北京二中组织同学去云南省春游,在地图上设定的临沧市位置点的坐标为(-1,0),出发点昆明市位置点的坐标为(1,1).如图请帮助小强确定出终点香格里拉位置点的坐标为(-1,4).
北京二中组织同学去云南省春游,在地图上设定的临沧市位置点的坐标为(-1,0),出发点昆明市位置点的坐标为(1,1).如图请帮助小强确定出终点香格里拉位置点的坐标为(-1,4).  53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:解答题
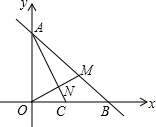 如图,直线y=-x+m与x轴交于点B(4,0),与y轴交于点A,点C为OB上一点,点M为AB上一点,OM交AC于N,S△ABC=4.
如图,直线y=-x+m与x轴交于点B(4,0),与y轴交于点A,点C为OB上一点,点M为AB上一点,OM交AC于N,S△ABC=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
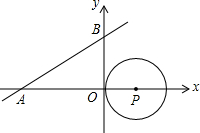 直线y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),圆P与y轴相切于点O.若将圆P沿x轴向左平移,当圆P与该直线相切时点P的坐标为(-1,0)或(-5,0);当圆P与该直线相交时,横坐标为整数的点P有3个.
直线y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),圆P与y轴相切于点O.若将圆P沿x轴向左平移,当圆P与该直线相切时点P的坐标为(-1,0)或(-5,0);当圆P与该直线相交时,横坐标为整数的点P有3个.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
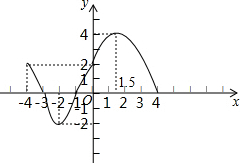 已知某一函数的全部图象如图所示,根据图象回答下列问题:
已知某一函数的全部图象如图所示,根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
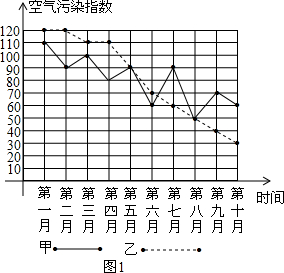 甲、乙两城市为了解决空气质量污染问题,对城市及其周边的环境污染进行了综合治理.在治理的过程中,环保部门每月初对两城市的空气质量进行监测,连续10个月的空气污染指数如图1所示.其中,空气污染指数≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.
甲、乙两城市为了解决空气质量污染问题,对城市及其周边的环境污染进行了综合治理.在治理的过程中,环保部门每月初对两城市的空气质量进行监测,连续10个月的空气污染指数如图1所示.其中,空气污染指数≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.| 平均数 | 方差 | 中位数 | 空气质量为优的次数 | |
| 甲 | 80 | 340 | 85 | 1 |
| 乙 | 80 | 1060 | 80 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com