

分析 由题意可知:第1次分割,把正方形的面积二等分,其中阴影部分的面积为$\frac{1}{2}$;第2次分割,把上次分割图中空白部分的面积继续二等分,阴影部分的面积之和为$\frac{1}{2}$+$\frac{1}{{2}^{2}}$=1-$\frac{1}{{2}^{2}}$;第3次分割,把上次分割图中空白部分的面积继续二等分…,第n次分割,把上次分割图中空白部分的面积最后二等分,所有阴影部分的面积之和为$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$,最后空白部分的面积是1-$\frac{1}{{2}^{n}}$,由此规律得出答案即可.
解答 解:∵第1次分割,影部分的面积为$\frac{1}{2}$;
第2次分割,阴影部分的面积之和为$\frac{1}{2}$+$\frac{1}{{2}^{2}}$=1-$\frac{1}{{2}^{2}}$;
…,
第n次分割,所有阴影部分的面积之和为$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$=1-$\frac{1}{{2}^{n}}$,
∴$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{2015}}$=1-$\frac{1}{{2}^{2015}}$.
故答案为:1-$\frac{1}{{2}^{2015}}$.
点评 此题考查了图形的变化规律,读懂题目信息,理解分割的方法以及求和的方法是解题的关键.


科目:初中数学 来源: 题型:填空题
 如图,线段AB的长为4,C为AB上一动点,分别以AC、BC为斜边在AB的同侧作等腰直角△ACD和等腰直角△BCE,那么DE长的最小值是2.
如图,线段AB的长为4,C为AB上一动点,分别以AC、BC为斜边在AB的同侧作等腰直角△ACD和等腰直角△BCE,那么DE长的最小值是2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
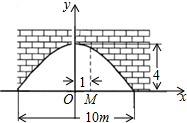 如图,有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m.把它的截面边缘的图形放在如图所示的直角坐标系中.在对称轴右边1m处,桥洞离水面的高是$\frac{99}{25}$m.
如图,有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m.把它的截面边缘的图形放在如图所示的直角坐标系中.在对称轴右边1m处,桥洞离水面的高是$\frac{99}{25}$m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
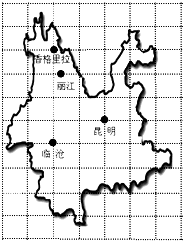 北京二中组织同学去云南省春游,在地图上设定的临沧市位置点的坐标为(-1,0),出发点昆明市位置点的坐标为(1,1).如图请帮助小强确定出终点香格里拉位置点的坐标为(-1,4).
北京二中组织同学去云南省春游,在地图上设定的临沧市位置点的坐标为(-1,0),出发点昆明市位置点的坐标为(1,1).如图请帮助小强确定出终点香格里拉位置点的坐标为(-1,4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
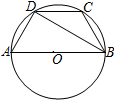 如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=6cm,∠ABD=30°,则⊙O的面积为( )
如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=6cm,∠ABD=30°,则⊙O的面积为( )| A. | 25πcm2 | B. | 49πcm2 | C. | 32πcm2 | D. | 36πcm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
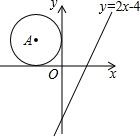 如图,在平面直角坐标系中,点A在第二象限,⊙A分别与x轴、y轴相切.若将⊙A向右平移5个单位,圆心A恰好落在直线y=2x-4上,则⊙A的半径为( )
如图,在平面直角坐标系中,点A在第二象限,⊙A分别与x轴、y轴相切.若将⊙A向右平移5个单位,圆心A恰好落在直线y=2x-4上,则⊙A的半径为( )| A. | $\frac{4}{3}$ | B. | 2 | C. | 4 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com