
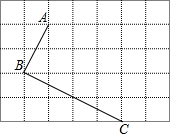
 如图,在方格纸中,每个小方格的边长为1,把线段AB沿BC方向平移BC的长度后,线段AB所扫过的面积是10.
如图,在方格纸中,每个小方格的边长为1,把线段AB沿BC方向平移BC的长度后,线段AB所扫过的面积是10. 分析 连结AC,如图,先利用勾股定理计算出AB=$\sqrt{5}$,BC=2$\sqrt{5}$,AC=5,则根据勾股定理的逆定理可判断△ABC为直角三角形,∠ABC=90°,再利用平移的性质得AB∥CD,AB=CD,于是可判断四边形ABCD为矩形,
然后根据矩形得面积公式求解.
解答 解: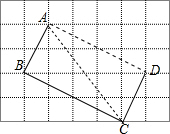 连结AC,如图,
连结AC,如图,
AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,BC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,AC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵($\sqrt{5}$)2+(2$\sqrt{5}$)2=52,
∴AB2+BC2=AC2,
∴△ABC为直角三角形,∠ABC=90°,
∵线段AB沿BC方向平移BC的长度后得到CD,
∴AB∥CD,AB=CD,
∴四边形ABCD为矩形,
∴线段AB所扫过的面积=S矩形ABCD=$\sqrt{5}$×2$\sqrt{5}$=10.
故答案为10.
点评 本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.也考查了勾股定理的逆定理.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是每个面上都有一个汉字的正方体的一种侧面展开图,那么在原正方体的表面上,与汉字“美”相对的面上的汉字是( )
如图是每个面上都有一个汉字的正方体的一种侧面展开图,那么在原正方体的表面上,与汉字“美”相对的面上的汉字是( )| A. | 我 | B. | 爱 | C. | 丹 | D. | 东 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
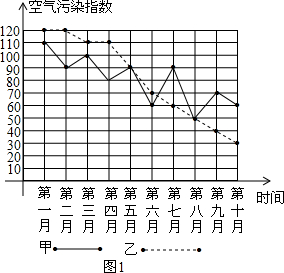 甲、乙两城市为了解决空气质量污染问题,对城市及其周边的环境污染进行了综合治理.在治理的过程中,环保部门每月初对两城市的空气质量进行监测,连续10个月的空气污染指数如图1所示.其中,空气污染指数≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.
甲、乙两城市为了解决空气质量污染问题,对城市及其周边的环境污染进行了综合治理.在治理的过程中,环保部门每月初对两城市的空气质量进行监测,连续10个月的空气污染指数如图1所示.其中,空气污染指数≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.| 平均数 | 方差 | 中位数 | 空气质量为优的次数 | |
| 甲 | 80 | 340 | 85 | 1 |
| 乙 | 80 | 1060 | 80 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com