
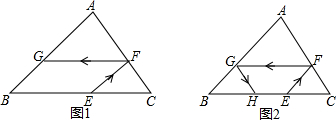
分析 (1))根据∠GFE=40°,求出∠EFC的度数,根据EF∥AB,FG∥BC,分别求出∠AFG、∠C、∠B、∠A的度数;
(2)根据已知条件证明△ABC是等边三角形,得到HD∥AB.
解答 解:(1)∵∠GFE=40°,∴∠EFC=∠AFG=(180°-40°)÷2=70°,
∵FG∥BC,∴∠C=∠AFG=70°,
∵EF∥AB,FG∥BC,∴四边形GFEB为平行四边形,
∴∠B=∠GFE=40°,
∠A=180°-∠B-∠C=70°,
故答案为70°;70°;40°;70°.
(2)∵GH∥AC,∴∠BGH=∠A,
∵FG∥BC,∴∠AGF=∠B,
∵∠AGF=∠BGH,
∴∠A=∠B,
同理,∠A=∠C,
∴△ABC是等边三角形,
∵GH∥AC,∴∠BGH=∠A=60°,
∴∠DHC=60°=∠B,
∴HD∥AB.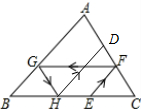
点评 本题考查了平行线的性质和判定的应用,解此题的关键是能正确作出辅助线,注意:平行线的性质是:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然,此题是一道中档题目,难度适中.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:填空题
 如图,线段AB的长为4,C为AB上一动点,分别以AC、BC为斜边在AB的同侧作等腰直角△ACD和等腰直角△BCE,那么DE长的最小值是2.
如图,线段AB的长为4,C为AB上一动点,分别以AC、BC为斜边在AB的同侧作等腰直角△ACD和等腰直角△BCE,那么DE长的最小值是2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
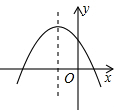 二次函数y=ax2+bx+c的图象如图,则函数y=$\frac{a}{x}$与函数y=bx在同一坐标系内的大致图象是( )
二次函数y=ax2+bx+c的图象如图,则函数y=$\frac{a}{x}$与函数y=bx在同一坐标系内的大致图象是( )| A. | 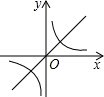 | B. | 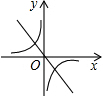 | C. |  | D. | 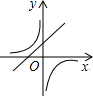 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 到凤凰社区供水点的路程(千米) | 运费(元/吨•千米) | |
| 甲厂 | 20 | 12 |
| 乙厂 | 14 | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
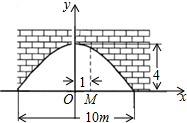 如图,有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m.把它的截面边缘的图形放在如图所示的直角坐标系中.在对称轴右边1m处,桥洞离水面的高是$\frac{99}{25}$m.
如图,有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m.把它的截面边缘的图形放在如图所示的直角坐标系中.在对称轴右边1m处,桥洞离水面的高是$\frac{99}{25}$m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
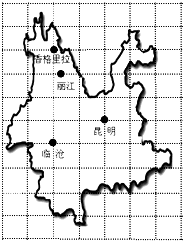 北京二中组织同学去云南省春游,在地图上设定的临沧市位置点的坐标为(-1,0),出发点昆明市位置点的坐标为(1,1).如图请帮助小强确定出终点香格里拉位置点的坐标为(-1,4).
北京二中组织同学去云南省春游,在地图上设定的临沧市位置点的坐标为(-1,0),出发点昆明市位置点的坐标为(1,1).如图请帮助小强确定出终点香格里拉位置点的坐标为(-1,4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com