
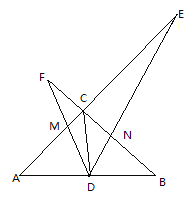
【题目】如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为E、F,DF与AC交于点M,DE与BC交于点N。
(1)求证:△ADM∽△BND;
(2)在∠EDF绕点D旋转的过程中:
①探究三条线段CD、CE、CF之间的数量关系,并说明理由;
②若CE=4,CF=2,求DN的长.
【答案】(1)(略),(2)①见解析,②![]() .
.
【解析】试题分析:(1)根据等腰直角三角形的性质得到∠BCD=∠ACD=45°,∠BCE=∠ACF=90°,于是得到∠DCE=∠DCF=135°,根据全等三角形的性质即可的结论;
(2)①证得△CDF∽△CED,根据相似三角形的性质得到![]() ,即CD2=CECF;
,即CD2=CECF;
②如图,过D作DG⊥BC于G,于是得到∠DGN=∠ECN=90°,CG=DG,当CE=4,CF=2时,求得CD=![]() ,推出△CEN∽△GDN,根据相似三角形的性质得到
,推出△CEN∽△GDN,根据相似三角形的性质得到![]() =2,根据勾股定理即可得到结论.
=2,根据勾股定理即可得到结论.
(1)证明:∵∠ACB=90°,AC=BC,AD=BD,∴∠BCD=∠ACD=45°,∠BCE=∠ACF=90°,∴∠DCE=∠DCF=135°,在△DCE与△DCF中,∵CE=CF,∠DCE=∠DCF,CD=CD,∴△DCE≌△DCF,∴DE=DF;
(2)解:①∵∠DCF=∠DCE=135°,∴∠CDF+∠F=180°﹣135°=45°,∵∠CDF+∠CDE=45°,∴∠F=∠CDE,∴△CDF∽△CED,∴ ![]() ,即CD2=CECF;
,即CD2=CECF;
②如图,过D作DG⊥BC于G,则∠DGN=∠ECN=90°,CG=DG,当CE=4,CF=2时,由CD2=CECF得CD=![]() ,∴在Rt△DCG中,CG=DG=CDsin∠DCG=
,∴在Rt△DCG中,CG=DG=CDsin∠DCG=![]() ×sin45°=2,∵∠ECN=∠DGN,∠ENC=∠DNG,∴△CEN∽△GDN,∴
×sin45°=2,∵∠ECN=∠DGN,∠ENC=∠DNG,∴△CEN∽△GDN,∴![]() =2,∴GN=
=2,∴GN=![]() CG=
CG=![]() ,∴DN=
,∴DN=![]() =
=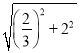 =
=![]() .
.



 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
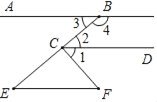
【题目】把下面的推理过程补充完整,并在括号内填上理由.
已知:B、C、E三点在一条直线上,∠3=∠E,∠4+∠2=180°.
试说明:∠BCF=∠E+∠F
解:∵∠3=∠E(已知)
∴EF∥ (内错角相等,两直线平行)
∵∠4+∠2=180°(已知)
∴CD∥
∴CD∥ (平行于同一条直线的两条直线互相平行)
∴∠1=∠F,
∠2=
∵∠BCF=∠1+∠2(已知)
∴∠BCF=∠E+∠F(等量代换)
查看答案和解析>>
科目:初中数学 来源: 题型:
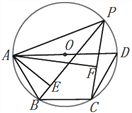
【题目】如图:点P是四边形ABCD外接圆⊙O上的任意一点,且不与四边形顶点重合,若AD是⊙O的直径,AB=BC=CD,连接PA,PB,PC,若PA= ![]() ,求点A到PB和PC的距离之和AE+AF是多少?
,求点A到PB和PC的距离之和AE+AF是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,AB=8cm,BC=16cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
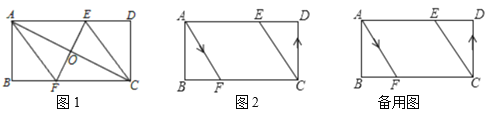
(1)如图1,连接AF、CE,判断四边形AFCE的形状,并说明理由;
(2)如图2,动点P、Q分别从A、C两点同时出发,P点沿着A→F→B→A匀速运动,Q点沿着C→D→E→C匀速运动,在运动过程中:
① 已知点P的速度为10cm/s,点Q的速度为8cm/s,运动时间为t秒,问当t为何值时,点A,C,P,Q组成的四边形为平行四边形?
② 点P,Q的运动路程分别为a,b(单位:cm,ab≠0),问当a,b满足怎样的关系式时,点A,C,P,Q组成的四边形为平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为了扩大经营,决定购进6台机器用于生产某活塞.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示.经过预算,本次购买机器所耗资金不能超过34万元.
甲 | 乙 | |
价格(万元/台) | 7 | 5 |
每台日产量(个) | 100 | 60 |
(1)按该公司要求可以有几种购买方案?
(2)如果该公司购进的6台机器的日生产能力不能低于380个,那么为了节约资金应选择什么样的购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了“迎国庆,向祖国母亲献礼”,某建筑公司承建了修筑一段公路的任务,指派甲、乙两队合作,18天可以完成,共需施工费126000元;如果甲、乙两队单独完成此项工程,乙队所用时间是甲队的1.5倍,乙队每天的施工费比甲队每天的施工费少1000元.
(1)甲、乙两队单独完成此项工程,各需多少天?
(2)为了尽快完成这项工程任务,甲、乙两队通过技术革新提高了速度,同时,甲队每天的施工费提高了![]() ,乙队每天的施工费提高了
,乙队每天的施工费提高了![]() ,已知两队合作12天后,由甲队再单独做2天就完成了这项工程任务,且所需施工费比计划少了21200元.
,已知两队合作12天后,由甲队再单独做2天就完成了这项工程任务,且所需施工费比计划少了21200元.
①分别求出甲、乙两队技术革新前每天的施工费用;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点,与y轴交于C点,已知点B坐标为(4,0).
的图象与x轴交于A、B两点,与y轴交于C点,已知点B坐标为(4,0).

(1)求抛物线的解析式;
(2)判断△ABC的形状,直接写出△ABC外接圆的圆心坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
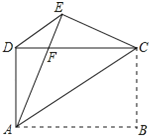
(1)求证:△DEC≌△EDA;
(2)求DF的值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com