
分析 (1)变形为(100-2)2,根据完全平方公式计算即可求解;
(2)根据完全平方公式和单项式乘以单项式的计算法则计算即可求解;
(3)先变形为(m-n)2-(m-n)2,再合并即可求解;
(4)先变形为[(3m+2)-2n][(3m+2)+2n],再根据完全平方公式计算即可求解.
解答 解:(1)982
=(100-2)2
=1002-2×100×2+22
=10000-400+4
=9604;
(2)(a-5)2-(a-2)(a+3)
=a2-10a+25-a2-a+6
=-11a+31;
(3)(m-n)2+(m-n)(n-m)
=(m-n)2-(m-n)2
=0;
(4)(3m-2n+2)(3m+2n+2)
=[(3m+2)-2n][(3m+2)+2n]
=(3m+2)2-4n2
=9m2+12m+4-4n2.
点评 此题考查了完全平方公式,平方差公式,单项式乘以单项式,关键是熟练掌握计算法则正确进行计算.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图:
如图:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
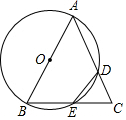 如图,在△ABC中,AB=AC,以AB为直径的圆分别交边AC,BC于点D,E,若$\widehat{AD}$=$\widehat{DE}$+30°,则∠DEC的度数是( )
如图,在△ABC中,AB=AC,以AB为直径的圆分别交边AC,BC于点D,E,若$\widehat{AD}$=$\widehat{DE}$+30°,则∠DEC的度数是( )| A. | 30° | B. | 40° | C. | 45° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com