
【题目】已知,点![]() 为二次函数
为二次函数![]() 图象的顶点,直线
图象的顶点,直线![]() 分别交
分别交![]() 轴正半轴,
轴正半轴,![]() 轴于点
轴于点![]() ,
,![]() .
.

(1)判断顶点![]() 是否在直线
是否在直线![]() 上,并说明理由.
上,并说明理由.
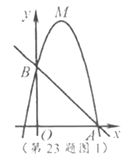
(2)如图1,若二次函数图象也经过点![]() ,
,![]() ,且
,且![]() ,根据图象,写出
,根据图象,写出![]() 的取值范围.
的取值范围.
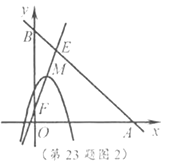
(3)如图2,点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 内,若点
内,若点![]() ,
,![]() 都在二次函数图象上,试比较
都在二次函数图象上,试比较![]() 与
与![]() 的大小.
的大小.
【答案】(1)点![]() 在直线
在直线![]() 上,理由见解析;(2)
上,理由见解析;(2)![]() 的取值范围为
的取值范围为![]() 或
或![]() .(3)①当
.(3)①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() ;③当
;③当![]() 时,
时,![]() .
.
【解析】(1)写出点![]() 的坐标,代入直线
的坐标,代入直线![]() 进行判断即可.
进行判断即可.
(2)直线![]() 与
与![]() 轴交于点为
轴交于点为![]() ,求出点
,求出点![]() 坐标,把
坐标,把![]() 在抛物线上,代入求得
在抛物线上,代入求得![]() ,求出二次函数表达式,进而求得点A的坐标,数形结合即可求出
,求出二次函数表达式,进而求得点A的坐标,数形结合即可求出![]() 时,
时,![]() 的取值范围.
的取值范围.
(3)直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,而直线
,而直线![]() 表达式为
表达式为![]() ,联立方程组
,联立方程组![]() ,得
,得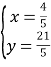 .点
.点![]() ,
,![]() .分三种情况进行讨论.
.分三种情况进行讨论.
【解答】
(1)∵点![]() 坐标是
坐标是![]() ,
,
∴把![]() 代入
代入![]() ,得
,得![]() ,
,
∴点![]() 在直线
在直线![]() 上.
上.
(2)如图1,∵直线![]() 与
与![]() 轴交于点为
轴交于点为![]() ,∴点
,∴点![]() 坐标为
坐标为![]() .
.
又∵![]() 在抛物线上,
在抛物线上,
∴![]() ,解得
,解得![]() ,
,
∴二次函数的表达式为![]() ,
,
∴当![]() 时,得
时,得![]() ,
,![]() ,∴
,∴![]() .
.
观察图象可得,当![]() 时,
时,
![]() 的取值范围为
的取值范围为![]() 或
或![]() .
.
(3)如图2,∵直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
而直线![]() 表达式为
表达式为![]() ,
,
解方程组![]() ,得
,得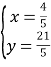 .∴点
.∴点![]() ,
,![]() .
.
∵点![]() 在
在![]() 内,
内,
∴![]() .
.
当点![]() ,
,![]() 关于抛物线对称轴(直线
关于抛物线对称轴(直线![]() )对称时,
)对称时,
![]() ,∴
,∴![]() .
.
且二次函数图象的开口向下,顶点![]() 在直线
在直线![]() 上,
上,
综上:①当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() ;
;
③当![]() 时,
时,![]() .
.


科目:初中数学 来源: 题型:
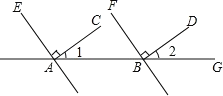
【题目】如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?
因为∠1=35°,∠2=35°(已知),所以∠1=∠2.所以___∥___( ).
又因为AC⊥AE(已知),所以∠EAC=90°( )
所以∠EAB=∠EAC+∠1=125°.
同理可得,∠FBG=∠FBD+∠2=__ °.
所以∠EAB=∠FBG( ).
所以___∥___(同位角相等,两直线平行).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
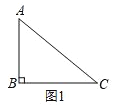
(1)如图1,在△ABC中,∠B=90,AB=3,BC=4,若△ABC的边上存在点P,使△ABP是以AB为腰的等腰三角形,则CP的长为______;
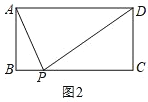
(2)如图2,在矩形ABCD中,AB=3,边BC上存在点P,使∠APD=90,求矩形ABCD面积的最小值.
问题解决:
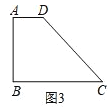
(3)如图3,在四边形ABCD中,AB=3,∠A=∠B=90,∠C=45,边CD上存在点P,使∠APB=60°,在此条件下,四边形ABCD的面积是否存在最大值?若存在,求出最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读第①小题的计算方法,再计算第②小题.
①–5![]() +(–9
+(–9![]() )+17
)+17![]() +(–3
+(–3![]() )
)
解:原式=[(–5)+(–![]() )]+[(–9)+(–
)]+[(–9)+(–![]() )]+(17+
)]+(17+![]() )+[(–3+(–
)+[(–3+(–![]() )]
)]
=[(–5)+(–9)+(–3)+17]+[(–![]() )+(–
)+(–![]() )+(–
)+(–![]() )+
)+![]() ]
]
=0+(–1![]() )
)
=–1![]() .
.
上述这种方法叫做拆项法.灵活运用加法的交换律、结合律可使运算简便.
②仿照上面的方法计算:(﹣2000![]() )+(﹣1999
)+(﹣1999![]() )+4000
)+4000![]() +(﹣1
+(﹣1![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小红玩抛硬币游戏,连续抛两次.小明说:“如果两次都是正面,那么你赢;如果两次是一正一反,则我赢.”小红赢的概率是__________,据此判断该游戏__________(填“公平”或“不公平”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 在平面直角坐标系内,顶点的坐标分别为
在平面直角坐标系内,顶点的坐标分别为![]() ,
,![]() 、
、![]() .
.
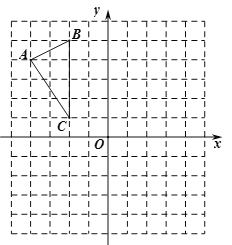
(1)平移![]() ,使点
,使点![]() 移到点
移到点![]() ,画出平移后的
,画出平移后的![]() ,并写出点
,并写出点![]() 的坐标.
的坐标.
(2)将![]() 绕点
绕点![]() 旋转
旋转![]() ,得到
,得到![]() ,画出旋转后的
,画出旋转后的![]() ,并写出点
,并写出点![]() 的坐标.
的坐标.
(3)求(2)中的点![]() 旋转到点
旋转到点![]() 时,点
时,点![]() 经过的路径长(结果保留
经过的路径长(结果保留![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“四书五经”是中国的“圣经”,“四书五经”是《大学》、《中庸》、《论语》和《孟子》(四书)及《诗经》、《尚书》、《易经》、《礼记》、《春秋》(五经)的总称,这是一部被中国人读了几千年的教科书,包含了中国古代的政治理想和治国之道,是我们了解中国古代社会的一把钥匙,学校计划分阶段引导学生读这些书,计划先购买《论语》和《孟子》供学生使用,已知用500元购买《孟子》的数量和用800元购买《论语》的数量相同,《孟子》的单价比《论语》的单价少15元.
(1)求《论语》和《孟子》这两种书的单价各是多少?
(2)学校准备一次性购买这两种书![]() 本,但总费用不超过
本,但总费用不超过![]() 元,那么这所学校最多购买多少本《论语》?
元,那么这所学校最多购买多少本《论语》?
查看答案和解析>>
科目:初中数学 来源: 题型:
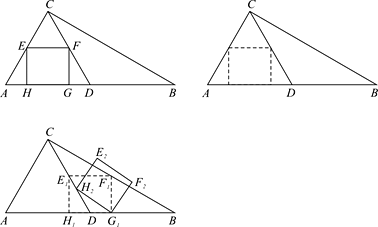
【题目】如图①,在△ABC中,∠ACB=90°,∠B=30°,AC=1,D为AB的中点,EF为△ACD 的中位线,四边形EFGH为△ACD的内接矩形(矩形的四个顶点均在△ACD的边上).
(1)计算矩形EFGH的面积;
(2)将矩形EFGH沿AB向右平移,F落在BC上时停止移动.在平移过程中,当矩形与△CBD重叠部分的面积为![]() 时,求矩形平移的距离;
时,求矩形平移的距离;
(3)如图③,将(2)中矩形平移停止时所得的矩形记为矩形![]() ,将矩形
,将矩形![]() 绕
绕![]() 点按顺时针方向旋转,当
点按顺时针方向旋转,当![]() 落在CD上时停止转动,旋转后的矩形记为矩形
落在CD上时停止转动,旋转后的矩形记为矩形![]() ,设旋转角为
,设旋转角为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上点A表示数a,点B表示数b,点C表示数c,b是最小的正整数,且a,c满足|a+2|+(c-7)2=0.
(1)填空:a=________,b=________,c=________;
(2)画出数轴,并把A,B,C三点表示在数轴上;
(3)P是数轴上任意一点,点P表示的数是x,当PA+PB+PC=10时,x的值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com