
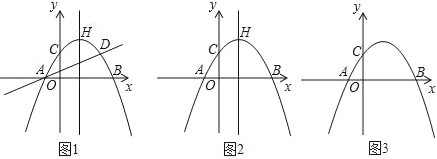
����Ŀ����ͼ��������y����![]() x2+bx+c��x�ύ��A����1��0����B��3��0������y�ύ��C�㣬��C���������ߵĶԳ���ĶԳƵ�Ϊ��D�������߶���ΪH��
x2+bx+c��x�ύ��A����1��0����B��3��0������y�ύ��C�㣬��C���������ߵĶԳ���ĶԳƵ�Ϊ��D�������߶���ΪH��
��1���������ߵĽ���ʽ��
��2������E�������ߵĶԳ������˶�ʱ����ֱ��AD���Ƿ���ڵ�F��ʹ���Ե�A��C��E��FΪ������ı���Ϊƽ���ı��Σ������ڣ��������F�����ꣻ�������ڣ���˵�����ɣ�
��3����PΪֱ��AD�Ϸ������ߵĶԳ�����һ���㣬����PA��PD����S��PAD��3������x���ϴ����Զ���Q��ʹPQ+![]() QB��С�������ڣ���ֱ��д����ʱ��Q�����꼰PQ+
QB��С�������ڣ���ֱ��д����ʱ��Q�����꼰PQ+![]() QB����Сֵ��
QB����Сֵ��
���𰸡���1��![]() ��2����0��
��2����0��![]() ����2��
����2��![]() ����2����
����2����![]() ����3����2.5��0��
����3����2.5��0��
��������
��1����A����1��0����B��3��0�������뵽�����ߵĽ���ʽ�����ɽ��
��2�����ڣ�������������ۣ���EF����ACƽ�Ƶõ���C��EΪ��Ӧ�㣬A��FΪ��Ӧ�㣬�ٰ�F�����ֱ��AD�Ľ���ʽΪy��![]() x+
x+![]() �����ɽ�����ͼ2��ʾ����ʱ��F���D�غϣ����ɽ�����ͼ3��ʾ������ƽ�ƵĹ��ɣ���֪��F�ĺ�����Ϊ��2��
�����ɽ�����ͼ2��ʾ����ʱ��F���D�غϣ����ɽ�����ͼ3��ʾ������ƽ�ƵĹ��ɣ���֪��F�ĺ�����Ϊ��2��
�������ʽ���ɽ��
��3����ͼ4��ʾ������B��AD��ƽ���߽������ߵĶԳ����ڵ�N������P��PH��ֱ��BN����x��Ľ��㼴Ϊ��Q����ֱ��BN�Ľ���ʽΪy��![]() x+b������B��3��0�������BN�Ľ���ʽ�������ý���ʽ���M,N��ֵ�������PQ+
x+b������B��3��0�������BN�Ľ���ʽ�������ý���ʽ���M,N��ֵ�������PQ+![]() QB��PQ+QH����P��Q��H���㹲��ʱ��PQ+
QB��PQ+QH����P��Q��H���㹲��ʱ��PQ+![]() QB��С����ΪPH�����ɽ��
QB��С����ΪPH�����ɽ��
��1����������y����![]() x2+bx+c��x�ύ��A����1��0����B��3��0����
x2+bx+c��x�ύ��A����1��0����B��3��0����
��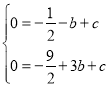 ��
��
��ã�![]() ��
��
�������ߵĽ���ʽΪ��![]() ��
��
��2�����ڣ�������������ۣ�
����ͼ1��ʾ��
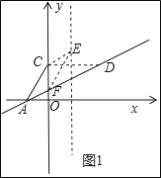
���ı���ACEFΪƽ���ı��Σ�
��EF����ACƽ�Ƶõ���C��EΪ��Ӧ�㣬A��FΪ��Ӧ�㣬
��C��0��![]() ������E�ĺ�����Ϊ1��
������E�ĺ�����Ϊ1��
������ƽ����һ����λ��
��A����1��0����
��F�ĺ�����Ϊ0��
��ֱ��AD�Ľ���ʽΪy��![]() x+
x+![]() ��
��
�൱x��0ʱ��y��![]() ��
��
��F��0��![]() ����
����
����ͼ2��ʾ��
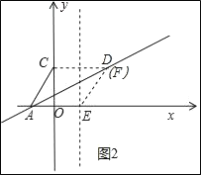
��ʱ��F���D�غϣ�
��F��2��![]() ����
����
����ͼ3��ʾ��
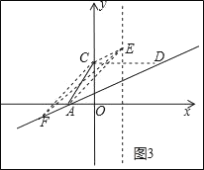
����ƽ�ƵĹ��ɣ���֪��F�ĺ�����Ϊ��2��
��x����2ʱ��y����![]() ��
��
��F����2����![]() ����
����
������������F��������0��![]() ����2��
����2��![]() ����2����
����2����![]() ����
����
��3����ͼ4��ʾ������B��AD��ƽ���߽������ߵĶԳ����ڵ�N������P��PH��ֱ��BN����x��Ľ��㼴Ϊ��Q��
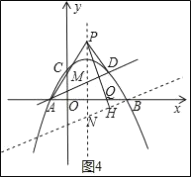
��ֱ��BN�Ľ���ʽΪy��![]() x+b������B��3��0����
x+b������B��3��0����
���b����![]() ��
��
��ֱ��BN�Ľ���ʽΪy��![]() x��
x��![]() ��
��
�������ߵĶԳ���Ϊֱ��x��1��
��N��1����1����
��ֱ��AD�������ߵĶԳ���Ľ���Ϊ��M��
��M��1��1����
��S��ADP��PM��xD��xA��![]() ��3��
��3��
��PM��2��
��P��1��3����
��tan��ABN��![]() ��
��
��![]() QB��QH��
QB��QH��
��PQ+![]() QB��PQ+QH��
QB��PQ+QH��
span>�൱P��Q��H���㹲��ʱ��PQ+![]() QB��С����ΪPH��
QB��С����ΪPH��
��PN��4����NPH����ABN��
��PH��![]() ��
��
��PQ+![]() QB����СֵΪ
QB����СֵΪ![]() ��
��
��ʱ��Q��2.5��0����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
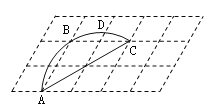
����Ŀ����ͼ��15����״��С��ȫ��ͬ����������������εĶ����Ϊ���. ��֪���ε�һ����Ϊ60�㣬A��B��C���ڸ���ϣ���D�ڹ�A��B��C�����Բ���ϣ���EҲ�ڸ���ϣ��ҡ�AED=��ACD����cos��AEC=________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ABC�ڽ��ڡ�O��AC��ֱ����D�ڡ�O�ϣ���ACƽ�֡�BCD��AE��BC����CD��E��F��CD���ӳ����ϣ���AE��EF������AF
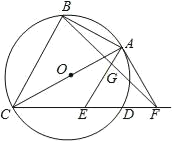
��1����֤��AF�ǡ�O�����ߣ�
��2������BF��AE��G����AB��12��AE��13����AG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������������8��00��ij������������˴�ͳ�ǰ�����麣��¡�����Σ����麣��¡�������������100ǧ�ף�������ij�������飬��8��30�Ӹ��������Լ�С���Դ��1.5�����ٶ��ϣ��ϴ�ͺ����ǰ�У�����ȸ���������ǰ20���ӵ������麣��¡����
��1�������С����ƽ���ٶȸ��Ƕ��٣�
��2��������ij�ϴ�͵ĵص㵽���麣��¡����·���ж�Զ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
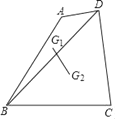
����Ŀ����ͼ��BD���ı���ABCD�ĶԽ��ߣ�AB��BC��6����ABC��60�㣬��G1��G2�ֱ��ǡ�ABD�͡�DBC�����ģ����G1��G2��ľ���Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������и��������������Բ��Թ���ϵͳ�����У�����������л���ͳ�ָ�Ϊ������Զ����ɣ��ֳ������ɼ�������������������ȣ���֤�˹�ƽ����ǰ����ʦΪ�˽�ȫ�г�������������Ŀ��ѡ�������ÿ����ѡһ�����ȫ�в��ֳ������������˵��飬���������ֳ����ࣺA��ʵ����![]() kg����B��������Զ��C��50���ܣ�D���볡����E���������������������Ƴ�����������������ͳ��ͼ���������ͳ��ͼ����������⣺
kg����B��������Զ��C��50���ܣ�D���볡����E���������������������Ƴ�����������������ͳ��ͼ���������ͳ��ͼ����������⣺
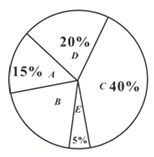
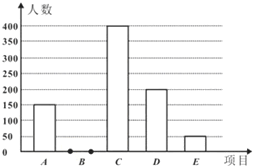
��1�������������ͳ��ͼ����������
��2���ٶ�ȫ�г�����ҵѧ������5500���������Թ���ȫ�г���������ѡ50���ܵ������ж����ˣ�
��3���ס���������������������ѡ���ʽϸߵ�������Ŀ��B��������Զ��C��50���ܣ�D���볡�����и�ѡһ�ͬʱѡ��볡����������Զ�ĸ����Ƕ��٣������б���������ͼ�ķ�������˵�����г����еȿ��ܵĽ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
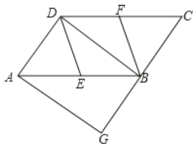
����Ŀ����ͼ����ƽ���ı���ABCD�У�E�� F�ֱ�Ϊ��AB��CD���е㣬BD�ǶԽ���.��������AG��DB��CB���ӳ����ڵ�G.
(1)��֤����ADE�ա�CBF��
(2)����G=90�� ,��֤:�ı���DEBF������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
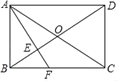
����Ŀ����ͼ���ھ���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AF��ֱƽ��OB����OB�ڵ�E����AB��6����CF�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
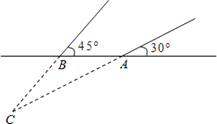
����Ŀ��2013��3�£�ijú������˹��ը���õؾ�Ԯ�������ϸ��ֳ����о�Ԯ����Ԯ����������̽�����ڵ���A��B����̽���̽�C��������������֪A��B�������4�ף�̽���������ļнǷֱ���30����45������ȷ���������ڵ�C����ȣ�����ȷ��0.1�ף��ο����ݣ�![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com