
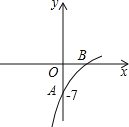
【题目】已知抛物线y=(1-a)x2+8x+b的图象的一部分如图所示,抛物线的顶点在第一象限,且经过点A(0,-7)和点B.
(1)求a的取值范围;
(2)若OA=2OB,求抛物线的解析式.
【答案】(1)a的取值范围是1<a<![]() ;(2)y=-
;(2)y=-![]() x2+8x-7.
x2+8x-7.
【解析】
(1)因为二次函数过点A,所以可以确定b的值,又因为抛物线为y=(1-a)x2+8x-7又抛物线的顶点在第一象限,开口向下,所以抛物线与x轴有两个不同的交点,所以可以确定1-a<0,△>0,解不等式组即可求得a的取值范围;
(2)因为OA=2OB,可求得点B的坐标,将点A,B的坐标代入二次函数的解析式即可求得a,b的值,即可求得二次函数的解析式.
(1)由图可知,b=-7.
故抛物线为y=(1-a)x2+8x-7.
又因抛物线的顶点在第一象限,开口向下,
所以抛物线与x轴有两个不同的交点.
∴ ,
,
解之,得1<a<![]() .
.
即a的取值范围是1<a<![]() .
.
(2)设B(x1,0),
由OA=20B,
得7=2x1,即x1=![]() .
.
由于x1=![]() ,方程(1-a)x2+8x-7=0的一个根,
,方程(1-a)x2+8x-7=0的一个根,
∴(1-a)(![]() )2+8×
)2+8×![]() -7=0
-7=0
∴![]() .
.
故所求所抛物线解析式为y=-![]() x2+8x-7.
x2+8x-7.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
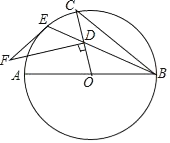
【题目】如图,AB是⊙O的直径,BE是弦,点D是弦BE上一点,连接OD并延长交⊙O于点C,连接BC,过点D作FD⊥OC交⊙O的切线EF于点F.
(1)求证:∠CBE=![]() ∠F;
∠F;
(2)若⊙O的半径是2![]() ,点D是OC中点,∠CBE=15°,求线段EF的长.
,点D是OC中点,∠CBE=15°,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
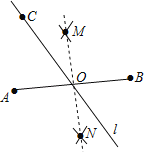
【题目】数学课上,老师提出如下问题:已知点A,B,C是不在同一直线上三点,求作一条过点C的直线l,使得点A,B到直线l的距离相等.
小明的作法如下:
①连接AB;
②分别以A,B为圆心,以大于![]() AB为半径画弧,两弧交于M、N两点;
AB为半径画弧,两弧交于M、N两点;
③作直线MN,交线段AB于点O;
④作直线CO,则CO就是所求作的直线l.
老师肯定了小明的作法,根据上面的作法回答下列问题:
(1)小明利用尺规作图作出的直线MN是线段AB的 ;点O是线段AB的 ;
(2)要证明点A,点B到直线l的距离相等,需要在图中画出必要的线段,请在图中作出辅助线,并说明线段 的长是点A到直线l的距离,线段 的长是点B到直线l的距离;
(3)证明点A,B到直线l的距离相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
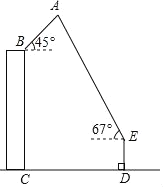
【题目】4月18日,一年一度的“风筝节”活动在市政广场举行,如图,广场上有一风筝A,小江抓着风筝线的一端站在D处,他从牵引端E测得风筝A的仰角为67°,同一时刻小芸在附近一座距地面30米高(BC=30米)的居民楼顶B处测得风筝A的仰角是45°,已知小江与居民楼的距离CD=40米,牵引端距地面高度DE=1.5米,根据以上条件计算风筝距地面的高度(结果精确到0.1米,参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.414).
≈1.414).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发市场香蕉的价格如下表
购买香蕉数(千克) | 不超过20千克 | 20千克以上但不超过40千克 | 40千克以上 |
每千克的价格 | 6元 | 5元 | 4元 |
张强两次共购买香蕉50千克,已知第二次购买的数量多于第一次购买的数量,共付出264元,请问张强第一次,第二次分别购买香蕉多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
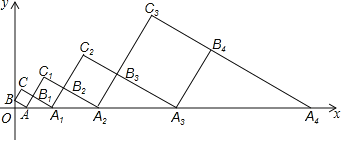
【题目】如图所示,在平面直角坐标系中,点A(![]() ,0)、B(0,
,0)、B(0,![]() ),以AB为边作正方形ABCB1,延长CB1交x轴于点A1,以A1B1为边作正方形A1B1C1B2,延长C1B2交x轴于点A2,以A2B2为边作正方形A2B2C2B3,延长C2B3交x轴于点A3,以A3B3为边作正方形A3B3C3B4,…,依此规律,则△A6B7A7的周长为_____.
),以AB为边作正方形ABCB1,延长CB1交x轴于点A1,以A1B1为边作正方形A1B1C1B2,延长C1B2交x轴于点A2,以A2B2为边作正方形A2B2C2B3,延长C2B3交x轴于点A3,以A3B3为边作正方形A3B3C3B4,…,依此规律,则△A6B7A7的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
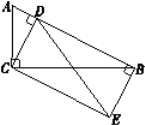
【题目】如图,在Rt△ABC中,![]() ,CD⊥AB于点D,BE⊥AB于点B,BE=CD,连接CE,DE.
,CD⊥AB于点D,BE⊥AB于点B,BE=CD,连接CE,DE.
(1)求证:四边形CDBE为矩形;
(2)若AC=2,![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京市环境保护监测中心每月向公众公布北京市各区域的空气质量状况.2019年1月份各区域的![]() 浓度情况如表:
浓度情况如表:
各区域1月份![]() 浓度(单位:微粒/立方米)表
浓度(单位:微粒/立方米)表
区域 |
| 区域 |
| 区域 |
|
怀柔 | 33 | 海淀 | 50 | 平谷 | 45 |
密云 | 34 | 延庆 | 51 | 丰台 | 61 |
门头沟 | 41 | 西城 | 61 | 大兴 | 72 |
顺义 | 41 | 东城 | 60 | 开发区 | 65 |
昌平 | 38 | 石景山 | 55 | 房山 | 62 |
朝阳 | 54 | 通州 | 57 |
从上述表格随机选择一个区域,其2019年1月份![]() 的浓度小于51微克/立方米的概率是______.
的浓度小于51微克/立方米的概率是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
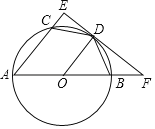
【题目】如图,已知AB为⊙O的直径,AC是⊙O的弦,D是弧BC的中点,过点D作⊙O的切线,分别交AC、AB的延长线于点E和点F,连接CD、BD.
(1)求证:∠A=2∠BDF;
(2)若AC=3,AB=5,求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com