
【题目】如图,AB是⊙O的直径,BE是弦,点D是弦BE上一点,连接OD并延长交⊙O于点C,连接BC,过点D作FD⊥OC交⊙O的切线EF于点F.
(1)求证:∠CBE=![]() ∠F;
∠F;
(2)若⊙O的半径是2![]() ,点D是OC中点,∠CBE=15°,求线段EF的长.
,点D是OC中点,∠CBE=15°,求线段EF的长.
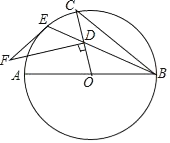
【答案】(1)详见解析;(2)![]()
【解析】
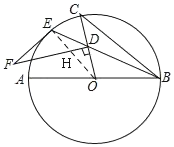
(1)连接OE交DF于点H,由切线的性质得出∠F+∠EHF =90,由FD⊥OC得出∠DOH+∠DHO =90,依据对顶角的定义得出∠EHF=∠DHO,从而求得∠F=∠DOH,依据∠CBE=![]() ∠DOH,从而即可得证;
∠DOH,从而即可得证;
(2)依据圆周角定理及其推论得出∠F=∠COE=2∠CBE =30°,求出OD的值,利用锐角三角函数的定义求出OH的值,进一步求得HE的值,利用锐角三角函数的定义进一步求得EF的值.
(1)证明:连接OE交DF于点H,
∵EF是⊙O的切线,OE是⊙O的半径,
∴OE⊥EF.
∴∠F+∠EHF=90°.
∵FD⊥OC,
∴∠DOH+∠DHO=90°.
∵∠EHF=∠DHO,
∴∠F=∠DOH.
∵∠CBE=![]() ∠DOH,
∠DOH,
∴![]()
(2)解:∵∠CBE=15°,
∴∠F=∠COE=2∠CBE=30°.
∵⊙O的半径是![]() ,点D是OC中点,
,点D是OC中点,
∴![]() .
.
在Rt△ODH中,cos∠DOH=![]() ,
,
∴OH=2.
∴![]() .
.
在Rt△FEH中,![]()
∴![]()


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
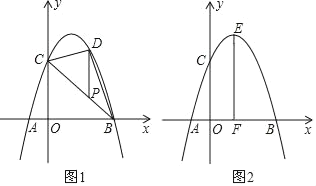
【题目】在平面直角坐标系xOy中抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
(1)求抛物线的表达式;
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BCD的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴于F点,N是线段EF上一动点,M(m,0)是x轴上一动点,若∠MNC=90°,直接写出实数m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
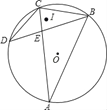
【题目】如图,已知△BAC为圆O内接三角形,AB=AC,D为⊙O上一点,连接CD、BD,BD与AC交于点E,且BC2=ACCE
①求证:∠CDB=∠CBD;
②若∠D=30°,且⊙O的半径为3+![]() ,I为△BCD内心,求OI的长.
,I为△BCD内心,求OI的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)试用含![]() 的代数式表示抛物线的顶点坐标;
的代数式表示抛物线的顶点坐标;
(2)将抛物线![]() 沿直线
沿直线![]() 翻折,得到的新抛物线与
翻折,得到的新抛物线与![]() 轴交于点
轴交于点![]() .若
.若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)已知![]() ,
,![]() ,在(2)的条件下,当线段
,在(2)的条件下,当线段![]() 与抛物线
与抛物线![]() 只有一个公共点时,直接写出
只有一个公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织学生到首钢西十冬奥广场开展综合实践活动,数学小组的同学们在距奥组委办公楼(原首钢老厂区的筒仓)20m的点B处,用高为0.8m的测角仪测得筒仓顶点C的仰角为63°,则筒仓CD的高约为______m.(精确到0.1m,sin63°≈0.89,cos63°≈0.45,tan63°≈1.96)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为2009年到2015年中关村国家自主创新示范区企业经营技术收入的统计图.下面四个推断:
①2009年到2015年技术收入持续增长;
②2009年到2015年技术收入的中位数是4032亿;
③2009年到2015年技术收入增幅最大的是2015年;
④2009年到2011年的技术收入增长的平均数比2013年到2015年技术收入增长的平均数大.
其中,正确的是( )
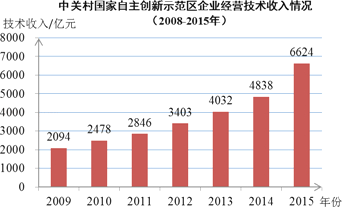
A.①③B.①④C.②③D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级共有8个班,241名同学,历史老师为了了解新中考模式下该校八年级学生选修历史学科的意向,请小红,小亮,小军三位同学分别进行抽样调查.三位同学调查结果反馈如下:

小红、小亮和小军三人中,你认为哪位同学的调查结果较好地反映了该校八年级同学选修历史的意向,请说出理由,并由此估计全年级有意向选修历史的同学的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和直线m,给出如下定义:若存在一点P,使得点P到直线m的距离等于1,则称P为直线m的平行点.
(1)当直线m的表达式为y=x时,
①在点![]() ,
,![]() ,
,![]() 中,直线m的平行点是______;
中,直线m的平行点是______;
②⊙O的半径为![]() ,点Q在⊙O上,若点Q为直线m的平行点,求点Q的坐标.
,点Q在⊙O上,若点Q为直线m的平行点,求点Q的坐标.
(2)点A的坐标为(n,0),⊙A半径等于1,若⊙A上存在直线![]() 的平行点,直接写出n的取值范围.
的平行点,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
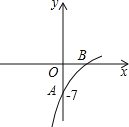
【题目】已知抛物线y=(1-a)x2+8x+b的图象的一部分如图所示,抛物线的顶点在第一象限,且经过点A(0,-7)和点B.
(1)求a的取值范围;
(2)若OA=2OB,求抛物线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com