
ΓΨΧβΡΩΓΩΡ≥―ß–ΘΦΤΜ°Ήι÷·»Ϊ–Θ1441Οϊ Π…ζΒΫœύΙΊ≤ΩΟ≈ΙφΜ°ΒΡΝ÷«χ÷≤ ςΘ§Ψ≠Ιΐ―–ΨΩΘ§ΨωΕ®Ήβ”ΟΒ±ΒΊΉβ≥ΒΙΪΥΨ“ΜΙ≤62ΝΨ![]() ΝΫ÷÷–ΆΚ≈ΩΆ≥ΒΉςΈΣΫΜΆ®ΙΛΨΏ.
ΝΫ÷÷–ΆΚ≈ΩΆ≥ΒΉςΈΣΫΜΆ®ΙΛΨΏ.
œ¬±μ «Ήβ≥ΒΙΪΥΨΧαΙ©Ηχ―ß–Θ”–ΙΊΝΫ÷÷–ΆΚ≈ΩΆ≥ΒΒΡ‘ΊΩΆΝΩΚΆΉβΫπ–≈œΔΘΚ
–ΆΚ≈ | ‘ΊΩΆΝΩ | ΉβΫπΒΞΦέ |
| 30»Υ/ΝΨ | 380‘Σ/ΝΨ |
| 20»Υ/ΝΨ | 280‘Σ/ΝΨ |
ΉΔΘΚ‘ΊΩΆΝΩ÷ΗΒΡ «ΟΩΝΨΩΆ≥ΒΉνΕύΩ…‘ΊΗΟ–Θ Π…ζΒΡ»Υ ΐ.…η―ß–ΘΉβ”Ο![]() –ΆΚ≈ΩΆ≥Β
–ΆΚ≈ΩΆ≥Β![]() ΝΨΘ§Ήβ≥ΒΉήΖ―”ΟΈΣ
ΝΨΘ§Ήβ≥ΒΉήΖ―”ΟΈΣ![]() ‘Σ.
‘Σ.
Θ®1Θ©«σ![]() ”κ
”κ![]() ΒΡΚ· ΐΫβΈω ΫΘ§«κ÷±Ϋ”–¥≥ω
ΒΡΚ· ΐΫβΈω ΫΘ§«κ÷±Ϋ”–¥≥ω![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©»τ“Σ ΙΉβ≥ΒΉήΖ―”Ο≤Μ≥§Ιΐ21940‘ΣΘ§“ΜΙ≤”–ΦΗ÷÷Ήβ≥ΒΖΫΑΗΘΩΡΡ÷÷Ήβ≥ΒΖΫΑΗΉήΖ―”ΟΉν ΓΘΩΉν ΓΒΡΉήΖ―”Ο «Εύ…ΌΘΩ
ΓΨ¥πΑΗΓΩ(1) 21ΓήxΓή62«“xΈΣ’ϊ ΐΘΜ(2)Ι≤”–25÷÷Ήβ≥ΒΖΫΑΗΘ§Β±Ήβ”ΟA–ΆΚ≈ΩΆ≥Β21ΝΨΘ§B–ΆΚ≈ΩΆ≥Β41ΝΨ ±Θ§ΉβΫπΉν…ΌΘ§ΈΣ19460‘ΣΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΉβ≥ΒΉήΖ―”Ο=AΓΔBΝΫ÷÷≥ΒΒΡΖ―”Ο÷°ΚΆΘ§Ν–≥ωΚ· ΐΙΊœΒ ΫΘ§‘ΌΗυΨίA
BΝΫ÷÷≥Β÷Ν…Ό“ΣΡήΉχ1441»ΥΦ¥Ω…ΒΟ»ΓxΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©”…ΉήΖ―”Ο≤Μ≥§Ιΐ21940‘ΣΩ…ΒΟΙΊ”ΎxΒΡ≤ΜΒ» ΫΘ§Ϋβ≤ΜΒ» ΫΚσ‘Όάϊ”ΟΚ· ΐΒΡ–‘÷ Φ¥Ω…ΫβΨωΈ Χβ.
(1)”…Χβ“βΒΟyΘΫ380xΘΪ280(62Θ≠x)ΘΫ100xΘΪ17360Θ§
ΓΏ30xΘΪ20(62Θ≠x)Γί1441Θ§
ΓύxΓί20.1Θ§Γύ21ΓήxΓή62«“xΈΣ’ϊ ΐΘΜ
(2)”…Χβ“βΒΟ100xΘΪ17360Γή21940Θ§
ΫβΒΟxΓή45.8Θ§Γύ21ΓήxΓή45«“xΈΣ’ϊ ΐΘ§
ΓύΙ≤”–25÷÷Ήβ≥ΒΖΫΑΗΘ§
ΓΏkΘΫ100>0Θ§ΓύyΥφxΒΡ‘ω¥σΕχ‘ω¥σΘ§
Β±xΘΫ21 ±Θ§y”–Ήν–Γ÷ΒΘ§ yΉν–ΓΘΫ100ΓΝ21ΘΪ17360ΘΫ19460Θ§
Ι Ι≤”–25÷÷Ήβ≥ΒΖΫΑΗΘ§Β±Ήβ”ΟA–ΆΚ≈ΩΆ≥Β21ΝΨΘ§B–ΆΚ≈ΩΆ≥Β41ΝΨ ±Θ§ΉβΫπΉν…ΌΘ§ΈΣ19460‘ΣΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
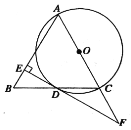
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ»γΆΦΘ§EΓΔF «ΥΡ±Ώ–ΈABCDΒΡΕ‘Ϋ«œΏAC…œΒΡΝΫΒψΘ§AF=CEΘ§DF=BEΘ§DFΓΈBEΘ°

«σ÷ΛΘΚΘ®1Θ©ΓςAFDΓ’ΓςCEBΘ°Θ®2Θ©ΥΡ±Ώ–ΈABCD «ΤΫ––ΥΡ±Ώ–ΈΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Εΰ¥ΈΚ· ΐ![]() ΒΡΆΦœσ”κy÷αΫΜ”ΎΒψCΘ§ΒψB «ΒψCΙΊ”ΎΗΟΕΰ¥ΈΚ· ΐΆΦœσΒΡΕ‘≥Τ÷αΕ‘≥ΤΒΡΒψ.“―÷Σ“Μ¥ΈΚ· ΐ
ΒΡΆΦœσ”κy÷αΫΜ”ΎΒψCΘ§ΒψB «ΒψCΙΊ”ΎΗΟΕΰ¥ΈΚ· ΐΆΦœσΒΡΕ‘≥Τ÷αΕ‘≥ΤΒΡΒψ.“―÷Σ“Μ¥ΈΚ· ΐ![]() ΒΡΆΦœσΨ≠ΙΐΗΟΕΰ¥ΈΚ· ΐΆΦœσ…œΒψ
ΒΡΆΦœσΨ≠ΙΐΗΟΕΰ¥ΈΚ· ΐΆΦœσ…œΒψ![]() ΦΑΒψB.
ΦΑΒψB.
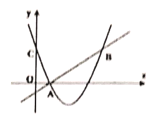
Θ®1Θ©«σBΒψΉχ±ξ”κΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΘΜ
Θ®2Θ©ΗυΨίΆΦœσΘ§–¥≥ω¬ζΉψ![]() ΒΡxΒΡ»Γ÷ΒΖΕΈß.
ΒΡxΒΡ»Γ÷ΒΖΕΈß.
Θ®3Θ©«σœΏΕΈ![]() ΒΡ≥ΛΕ».
ΒΡ≥ΛΕ».
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ»γΆΦΘ§‘ΎΓςABC÷–Θ§![]() Θ§“‘
Θ§“‘![]() ΈΣ÷±ΨΕΒΡΓ―O”κ
ΈΣ÷±ΨΕΒΡΓ―O”κ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() Θ§
Θ§![]() Θ§¥ΙΉψΈΣ
Θ§¥ΙΉψΈΣ![]() Θ§
Θ§![]() ΒΡ―”≥ΛœΏ”κ
ΒΡ―”≥ΛœΏ”κ![]() ΒΡ―”≥ΛœΏΫΜ”ΎΒψ
ΒΡ―”≥ΛœΏΫΜ”ΎΒψ![]() Θ°
Θ°
Θ®1Θ©«σ÷ΛΘΚ![]() «Γ―OΒΡ«–œΏ.
«Γ―OΒΡ«–œΏ.
Θ®2Θ©»τΓ―OΒΡΑκΨΕΈΣ4Θ§![]() Θ§«σ
Θ§«σ![]() ΒΡ≥ΛΘ°
ΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏ![]() ΒΡΕ‘≥Τ÷αΈΣ
ΒΡΕ‘≥Τ÷αΈΣ![]() Θ§”κ
Θ§”κ![]() ÷αΒΡ“ΜΗωΫΜΒψ‘Ύ
÷αΒΡ“ΜΗωΫΜΒψ‘Ύ![]() ΚΆ
ΚΆ![]() ÷°ΦδΘ§Τδ≤ΩΖ÷ΆΦœώ»γΆΦΥυ ΨΘ§‘ρœ¬Ν–Ϋα¬έΘΚΔΌΒψ
÷°ΦδΘ§Τδ≤ΩΖ÷ΆΦœώ»γΆΦΥυ ΨΘ§‘ρœ¬Ν–Ϋα¬έΘΚΔΌΒψ![]() Θ§
Θ§![]() Θ§
Θ§![]() «ΗΟ≈ΉΈοœΏ…œΒΡΒψΘ§‘ρ
«ΗΟ≈ΉΈοœΏ…œΒΡΒψΘ§‘ρ![]() ΘΜΔΎ
ΘΜΔΎ![]() ΘΜΔέ
ΘΜΔέ![]() Θ®
Θ®![]() ΈΣ»Έ“β Β ΐΘ©.Τδ÷–’ΐ»ΖΫα¬έΒΡΗω ΐ «Θ® Θ©
ΈΣ»Έ“β Β ΐΘ©.Τδ÷–’ΐ»ΖΫα¬έΒΡΗω ΐ «Θ® Θ©
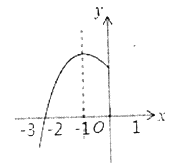
A. 0B. 1C. 2D. 3
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΙΊ”ΎxΒΡΖΫ≥ΧΘ®a©¹1Θ©x2+2x+a©¹1=0Θ°
Θ®1Θ©»τΗΟΖΫ≥Χ”–“ΜΗυΈΣ2Θ§«σaΒΡ÷ΒΦΑΖΫ≥ΧΒΡΝμ“ΜΗυΘΜ
Θ®2Θ©Β±aΈΣΚΈ÷Β ±Θ§ΖΫ≥ΧΫω”–“ΜΗωΗυΘΩ«σ≥ω¥Υ ±aΒΡ÷ΒΦΑΖΫ≥ΧΒΡΗυΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ Ώ≤Υ…ζ≤ζΜυΒΊΒΡΤχΈ¬ΫœΒΆ ±Θ§”ΟΉΑ”–ΚψΈ¬œΒΆ≥ΒΡ¥σ≈ο‘‘≈ύ“Μ÷÷–¬ΤΖ÷÷ Ώ≤ΥΘ°»γΆΦ « ‘―ιΫΉΕΈΒΡΡ≥ΧλΚψΈ¬œΒΆ≥¥”ΩΣΤτΒΫΙΊ±’ΚσΘ§¥σ≈οΡΎΒΡΈ¬Ε»y Θ®ΓφΘ©”κ ±ΦδxΘ®hΘ©÷°ΦδΒΡΚ· ΐΙΊœΒΘ§Τδ÷–œΏΕΈABΓΔBC±μ ΨΚψΈ¬œΒΆ≥ΩΣΤτΫΉΕΈΘ§ΥΪ«ζœΏΒΡ“Μ≤ΩΖ÷CD±μ ΨΚψΈ¬œΒΆ≥ΙΊ±’ΫΉΕΈΘ°
«κΗυΨίΆΦ÷––≈œΔΫβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©«σ’βΧλΒΡΈ¬Ε»y”κ ±ΦδxΘ®0ΓήxΓή24Θ©ΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®2Θ©«σΚψΈ¬œΒΆ≥…ηΕ®ΒΡΚψΕ®Έ¬Ε»ΘΜ
Θ®3Θ©»τ¥σ≈οΡΎΒΡΈ¬Ε»ΒΆ”Ύ10Γφ ±Θ§ Ώ≤ΥΜα ήΒΫ…ΥΚΠΘ°Έ ’βΧλΡΎΘ§ΚψΈ¬œΒΆ≥ΉνΕύΩ…“‘ΙΊ±’Εύ…Ό–Γ ±Θ§≤≈Ρή Ι Ώ≤Υ±ήΟβ ήΒΫ…ΥΚΠΘΩ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν–Τϊ≥Β±ξ÷Ψ÷–Θ§ «÷––ΡΕ‘≥ΤΆΦ–ΈΒΡ «Θ®ΓΓΓΓΘ©
A.  B.
B.  C.
C. ![]() D.
D. ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΨΊ–ΈABCD÷–Θ§![]() Θ§
Θ§![]() Θ§œ÷”–ΝΫ÷Μ¬λ“œPΚΆQΆ§ ±Ζ÷±π¥”AΓΔB≥ωΖΔΘ§―Ί
Θ§œ÷”–ΝΫ÷Μ¬λ“œPΚΆQΆ§ ±Ζ÷±π¥”AΓΔB≥ωΖΔΘ§―Ί![]() ΖΫœρ«ΑΫχΘ§¬λ“œPΟΩΟκΉΏ1cmΘ§¬λ“œQΟΩΟκΉΏ2cmΘ°Έ ΘΚ
ΖΫœρ«ΑΫχΘ§¬λ“œPΟΩΟκΉΏ1cmΘ§¬λ“œQΟΩΟκΉΏ2cmΘ°Έ ΘΚ
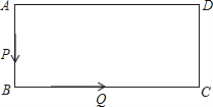

Θ®1Θ©¬λ“œ≥ωΖΔΚσΓςPBQΒΎ“Μ¥Έ «Β»―ϋ»ΐΫ«–Έ–η“Σ≈ά––ΦΗΟκ?
Θ®2Θ©PΓΔQΝΫ÷Μ¬λ“œΉνΩλ≈ά––ΦΗΟκΚσΘ§÷±œΏPQ”κ±ΏABΤΫ––?
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com