
【题目】已知抛物线![]() 的对称轴为
的对称轴为![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,其部分图像如图所示,则下列结论:①点
之间,其部分图像如图所示,则下列结论:①点![]() ,
,![]() ,
,![]() 是该抛物线上的点,则
是该抛物线上的点,则![]() ;②
;②![]() ;③
;③![]() (
(![]() 为任意实数).其中正确结论的个数是( )
为任意实数).其中正确结论的个数是( )
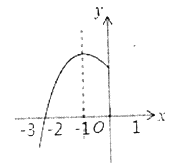
A. 0B. 1C. 2D. 3
【答案】C
【解析】
逐一分析3条结论是否正确:①根据抛物线的对称性找出点(-![]() ,y3)在抛物线上,再结合抛物线对称轴左边的单调性即可得出①错误;②由x=-3时,y<0,即可得出9a-3b+c<0,根据抛物线的对称轴为x=-1,即可得出b=2a,即可得出②正确;③∵抛物线开口向下,对称轴为x=-1,有最大值
,y3)在抛物线上,再结合抛物线对称轴左边的单调性即可得出①错误;②由x=-3时,y<0,即可得出9a-3b+c<0,根据抛物线的对称轴为x=-1,即可得出b=2a,即可得出②正确;③∵抛物线开口向下,对称轴为x=-1,有最大值![]() ,再根据x=t时的函数值为at2+bt+c,由此即可得出③正确.综上即可得出结论.
,再根据x=t时的函数值为at2+bt+c,由此即可得出③正确.综上即可得出结论.
解:①∵抛物线的对称轴为x=-1,点(![]() ,y3)在抛物线上,
,y3)在抛物线上,
∴(-![]() ,y3)在抛物线上.
,y3)在抛物线上.
∵-![]() <-
<-![]() <-
<-![]() ,且抛物线对称轴左边图象y值随x的增大而增大,
,且抛物线对称轴左边图象y值随x的增大而增大,
∴y1<y3<y2.∴①错误;
②∵抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,
∴-![]() =-1,∴2a=b,∴a=
=-1,∴2a=b,∴a=![]()
∵当x=-3时,y=9a-3b+c<0,
∴9![]() -3b+c=
-3b+c=![]() <0,
<0,
∴3b+2c<0,∴②正确;
③∵抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,开口向下
∴当x=-1,![]()
∵当x=t时,y= at2+bt+c
∵![]() 为任意实数
为任意实数
∴at2+bt+c≤![]()
∴at2+bt≤a-b.
∴③正确.
故选:C.


科目:初中数学 来源: 题型:
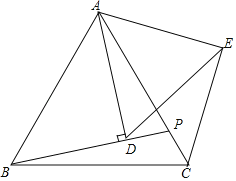
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,点P是线段AC上一动点(点P不与A,C重合),连接BP,过点A作直线BP的垂线段,垂足为点D,将线段AD绕点A逆时针旋转60°得到线段AE,连接DE,CE.
(1)求证:BD=CE;
(2)延长ED交BC于点F,求证:F为BC的中点;
(3)在(2)的条件下,若△ABC的边长为1,直接写出EF的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
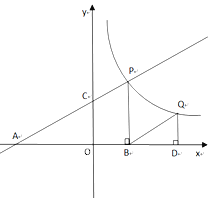
【题目】如图,直线y=![]() x+3分别交 x轴、y轴于点A、C.点P是该直线与双曲线在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=16.
x+3分别交 x轴、y轴于点A、C.点P是该直线与双曲线在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=16.
(1)求证:△AOC∽△ABP;
(2)求点P的坐标;
(3)设点Q与点P在同一个反比例函数的图象上,且点Q在直线PB的右侧,作QD⊥x轴于D,当△BQD与△AOC相似时,求点Q的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划组织全校1441名师生到相关部门规划的林区植树,经过研究,决定租用当地租车公司一共62辆![]() 两种型号客车作为交通工具.
两种型号客车作为交通工具.
下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 | 载客量 | 租金单价 |
| 30人/辆 | 380元/辆 |
| 20人/辆 | 280元/辆 |
注:载客量指的是每辆客车最多可载该校师生的人数.设学校租用![]() 型号客车
型号客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.
元.
(1)求![]() 与
与![]() 的函数解析式,请直接写出
的函数解析式,请直接写出![]() 的取值范围;
的取值范围;
(2)若要使租车总费用不超过21940元,一共有几种租车方案?哪种租车方案总费用最省?最省的总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌
粽子,每盒进价是40元,超市规定每盒售价不得少于45元.根据以往销售经验发现:当售价定为每盒45元时,每天可卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价![]() (元)之间的函数关系式;(4分)
(元)之间的函数关系式;(4分)
(2)当每盒售价定为多少元时,每天销售的利润![]() (元)最大?最大利润是多少?(6分)
(元)最大?最大利润是多少?(6分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b=0;③m为任意实数,则a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.其中正确的有( )
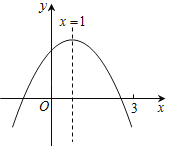
A.①②③B.②④C.②⑤D.②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,矩形ABCD的对角线AC、BD交于点O,过点C作BD的平行线,过点D作AC的平行线,两线交于点P,则四边形CODP的形状是 ;
(2)如图2,若题目中的矩形变为菱形,则四边形CODP的形状是 ;
(3)如图3,若题目中的矩形变为正方形,请判断四边形CODP的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com