
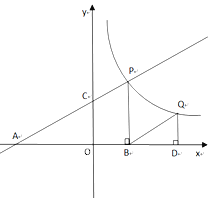
【题目】如图,直线y=![]() x+3分别交 x轴、y轴于点A、C.点P是该直线与双曲线在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=16.
x+3分别交 x轴、y轴于点A、C.点P是该直线与双曲线在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=16.
(1)求证:△AOC∽△ABP;
(2)求点P的坐标;
(3)设点Q与点P在同一个反比例函数的图象上,且点Q在直线PB的右侧,作QD⊥x轴于D,当△BQD与△AOC相似时,求点Q的横坐标.
【答案】(1)证明见解析;(2)点P的坐标为(2,4);(3)点Q的横坐标为:![]() 或
或![]() .
.
【解析】
(1)利用PB∥OC,即可证明三角形相似;
(2)由一次函数解析式,先求点A、C的坐标,由△AOC∽△ABP,利用线段比求出BP,AB的值,从而可求出点P的坐标即可;
(3)把P坐标代入求出反比例函数,设Q点坐标为(n,![]() ),根据△BQD与△AOC相似分两种情况,利用线段比联立方程组求出n的值,即可确定出Q坐标.
),根据△BQD与△AOC相似分两种情况,利用线段比联立方程组求出n的值,即可确定出Q坐标.
(1)证明:∵PB⊥ x轴,OC⊥x轴,
∴OC∥PB,
∴△AOC∽△ABP;
(2)解:对于直线y=![]() x+3,
x+3,
令x=0,得y=3;
令 y=0,得x=-6 ;
∴A(-6,0),C(0,4),
∴OA=6,OC=3.
∵△AOC∽△ABP,
∴ ,
,
∵S△ABP=16,S△AOC=![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴PB=4,AB=8,
∴OB=2,
∴点P的坐标为:(2,4).
(3)设反比例函数的解析式为:y=![]() ,
,
把P(2,4)代入,得k=xy=2×4=8,
∴y=![]() .
.
点Q在双曲线上,可设点Q的坐标为:(n,![]() )(n>2),
)(n>2),
则BD=![]() ,QD=
,QD=![]() ,
,
①当△BQD∽△ACO时,![]() ,
,
即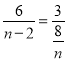 ,
,
整理得:![]() ,
,
解得:![]() 或
或![]() ;
;
②当△BQD∽△CAO时,![]() ,
,
即 ,
,
整理得:![]() ,
,
解得:![]() ,
,![]() (舍去),
(舍去),
综上①②所述,点Q的横坐标为:1+![]() 或1+
或1+![]() .
.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】某中学为了了解本校学生喜爱的球类运动,在本校范围内随机抽查了部分学生,将收集的数据统计整理,绘制成如下两幅不完整的统计图.
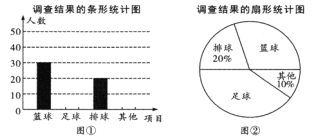
请你根据图中提供的信息解答下列问题:
(1)本次一共调查了________名学生;
(2)补全条形统计图;
(3) “足球”在扇形统计图中所占圆心角的度数为________;
(4)若已知该校有1000名学生,请你根据调查的结果估计爱好“足球”和“排球”的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个自然数从高位到个位是由一个数字或几个数字重复出现组成的,那么我们把这样的自然数叫做循环数,重复的一个或几个数字称为“循环节”,我们把“循环节”的数字个数叫做循环节的阶数.例如:525252,它由“52”依次重复出现组成,所以525252是循环数,它是2阶6位循环数.再如:77,是1阶2位循环数,135135135是3阶9位循环数.
(1)请直接写出1个2阶4位循环数 ,并证明对于任意一个2阶4位循环数,若交换其循环节的数字得到一个新的4位数,则该新数和原数的差能够被9整除.
(2)已知一个能被9整除的2阶4位数.设循环节为ab,且满足a﹣2b为非负偶数,求这个4位循环数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数
的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数![]() 的图象经过该二次函数图象上点
的图象经过该二次函数图象上点![]() 及点B.
及点B.
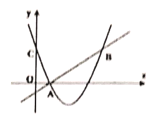
(1)求B点坐标与二次函数的解析式;
(2)根据图象,写出满足![]() 的x的取值范围.
的x的取值范围.
(3)求线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,![]() ,以
,以![]() 为直径的⊙O与
为直径的⊙O与![]() 交于点
交于点![]() ,
,![]() ,垂足为
,垂足为![]() ,
,![]() 的延长线与
的延长线与![]() 的延长线交于点
的延长线交于点![]() .
.
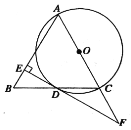
(1)求证:![]() 是⊙O的切线.
是⊙O的切线.
(2)若⊙O的半径为4,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的对称轴为
的对称轴为![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,其部分图像如图所示,则下列结论:①点
之间,其部分图像如图所示,则下列结论:①点![]() ,
,![]() ,
,![]() 是该抛物线上的点,则
是该抛物线上的点,则![]() ;②
;②![]() ;③
;③![]() (
(![]() 为任意实数).其中正确结论的个数是( )
为任意实数).其中正确结论的个数是( )
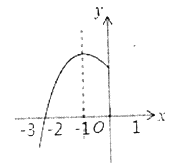
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y (℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在四边形![]() 中,
中,![]() 于点
于点![]() ,
,![]() ,点
,点![]() 为
为![]() 中点,
中点,![]() 为线段
为线段![]() 上的点,且
上的点,且![]() .
.
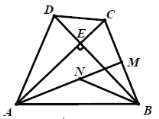
(1)求证:![]() 平分
平分![]() ;
;
(2)若![]() ,连接
,连接![]() ,当四边形
,当四边形![]() 为平行四边形时,求线段
为平行四边形时,求线段![]() 的长;
的长;
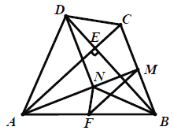
(3)若点![]() 为
为![]() 的中点,连接
的中点,连接![]() 、
、![]() (如图②),求证:
(如图②),求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com