
【题目】如果一个自然数从高位到个位是由一个数字或几个数字重复出现组成的,那么我们把这样的自然数叫做循环数,重复的一个或几个数字称为“循环节”,我们把“循环节”的数字个数叫做循环节的阶数.例如:525252,它由“52”依次重复出现组成,所以525252是循环数,它是2阶6位循环数.再如:77,是1阶2位循环数,135135135是3阶9位循环数.
(1)请直接写出1个2阶4位循环数 ,并证明对于任意一个2阶4位循环数,若交换其循环节的数字得到一个新的4位数,则该新数和原数的差能够被9整除.
(2)已知一个能被9整除的2阶4位数.设循环节为ab,且满足a﹣2b为非负偶数,求这个4位循环数.
【答案】(1)7171,证明见解析;(2)这个4位循环数为6363或8181.
【解析】
(1)根据循环节”的数字个数叫做循环节的阶数,可得答案;
(2)根据一个能被9整除的2阶4位循环数,可得![]() 能被9整除,即(a+b)能被9整除,得到a+b=9或a+b=18,根据a﹣2b为非负偶数,分类讨论可得答案.
能被9整除,即(a+b)能被9整除,得到a+b=9或a+b=18,根据a﹣2b为非负偶数,分类讨论可得答案.
(1)7171是2阶4位循环数;
证明:设原数为![]() ,新数为
,新数为![]() 即原数1000a+100b+10a+b,新数是1000b+100a+10b+a,
即原数1000a+100b+10a+b,新数是1000b+100a+10b+a,
1000b+100a+10b+a﹣(1000a+100b+10a+b)
=909b﹣909a
=909(b﹣a)
=9×101(b﹣a).
∵a,b为整数,
∴b﹣a也为整数,
∴新数和原数的差能够被9整除.
故答案为:7171.
(2)该2阶4位循环数为![]() ,
,
即![]() 112a+11b
112a+11b![]() ,
,
要使得1010a+101b能被9整除,则需(a+b)能被9整除.
∵0<a≤9,0<b≤9,
∴0<a+b≤18,
∴a,b应满足的关系是a+b=9或a+b=18.
①当a+b=9,即a=9-b时,
又∵a﹣2b为非负偶数,
∴9-b-2b≥0,
∴b≤3.
∵b为正整数,
∴b=1,2,3.
当b=1时,a=8,a-2b=8-2=6是非负偶数,满足条件;
当b=2时,a=7,a-2b=7-4=3不是非负偶数,不满足条件;
当b=3时,a=6,a-2b=6-6=0是非负偶数,满足条件;
∴这个4位循环数为8181或6363.
②当a+b=18,即a=18-b时,a=b=9,此时a-2b=-9不是非负偶数,不满足条件.
综上所述:这个4位循环数为6363或8181.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】韬韬想在春节期间去外地过年,爸爸对韬韬说:你从背面朝上且相同,正面分别写有1、2、3的三张卡片中随机摸出一张卡片不放回,然后再随机摸出另一张卡片,若两次摸出的数字之和等于4,则满足你的愿望.
(1)采用画树状图法或列表法列出两次摸出卡片的所有可能结果;
(2)韬韬实现愿望的概率有多大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展了主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调查,将他们的得分按优秀、良好、合格、不合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.
等级 | 频数 | 频率 |
优秀 | 20 |
|
良好 | ||
合格 | 10 |
|
不合格 | 5 |
|
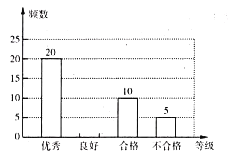
请根据以上信息,解答下列问题:
(1)本次调查随机抽取了______名学生;表中![]() ______,
______,![]() ______;
______;
(2)补全条形统计图;
(3)若全校有2000名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
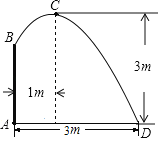
【题目】如图,在喷水池的中心A处竖直安装一个水管AB,水管的顶端安有一个喷水池,使喷出的抛物线形水柱在与池中心A的水平距离为1m处达到最高点![]() ,高度为3m,水柱落地点D离池中心A处3m,以水平方向为
,高度为3m,水柱落地点D离池中心A处3m,以水平方向为![]() 轴,建立平面直角坐标系,若选取
轴,建立平面直角坐标系,若选取![]() 点为坐标原点时的抛物线的表达式为
点为坐标原点时的抛物线的表达式为![]() ,则选取点
,则选取点![]() 为坐标原点时的抛物线表达式为______,水管
为坐标原点时的抛物线表达式为______,水管![]() 的长为______
的长为______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
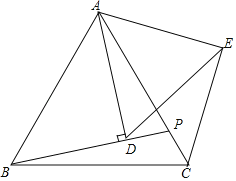
【题目】如图,△ABC为等边三角形,点P是线段AC上一动点(点P不与A,C重合),连接BP,过点A作直线BP的垂线段,垂足为点D,将线段AD绕点A逆时针旋转60°得到线段AE,连接DE,CE.
(1)求证:BD=CE;
(2)延长ED交BC于点F,求证:F为BC的中点;
(3)在(2)的条件下,若△ABC的边长为1,直接写出EF的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
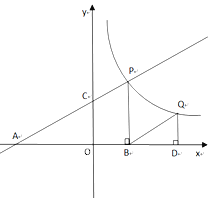
【题目】如图,直线y=![]() x+3分别交 x轴、y轴于点A、C.点P是该直线与双曲线在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=16.
x+3分别交 x轴、y轴于点A、C.点P是该直线与双曲线在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=16.
(1)求证:△AOC∽△ABP;
(2)求点P的坐标;
(3)设点Q与点P在同一个反比例函数的图象上,且点Q在直线PB的右侧,作QD⊥x轴于D,当△BQD与△AOC相似时,求点Q的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b=0;③m为任意实数,则a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.其中正确的有( )
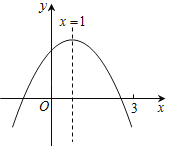
A.①②③B.②④C.②⑤D.②③⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com