
【题目】如图,△ABC为等边三角形,点P是线段AC上一动点(点P不与A,C重合),连接BP,过点A作直线BP的垂线段,垂足为点D,将线段AD绕点A逆时针旋转60°得到线段AE,连接DE,CE.
(1)求证:BD=CE;
(2)延长ED交BC于点F,求证:F为BC的中点;
(3)在(2)的条件下,若△ABC的边长为1,直接写出EF的最大值.
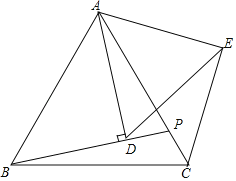
【答案】(1)见解析;(2)见解析;(3)1
【解析】
(1)由等边三角形的性质和旋转的性质可得∠DAB=∠CAE,AB=AC,AD=AE,即可证△ADB≌△AEC,可得BD=CE;
(2)过点C作CG//BP,交EF的延长线于点G,由等边三角形的性质和全等三角形的性质可得CG=BD,∠BDG=∠G,∠BFD=∠GFC,可证△BFD≌△CFG,可得结论;
(3)由题意可证点A,点F,点C,点E四点在以AC为直径的圆上,由直径是圆的最大弦可得EF的最大值.
证明:(1)∵将线段AD绕点A逆时针旋转60°得到线段AE
∴AD=AE,∠DAE=60°
∴△ADE是等边三角形
∵△ABC为等边三角形
∴AB=AC, ∠BAC=∠DAE=60°
∴∠DAB=∠CAE,且AB=AC,AD=AE
∴△ADB≌△AEC(SAS)
∴BD=CE
(2)如图,过点C作CG∥BP,交EF的延长线于点G
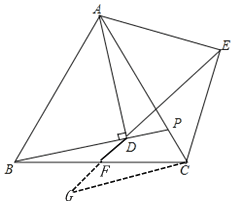
∵∠ADB=90°, ∠ADE=60°
∴∠BDG=30°
∵CG∥BP
∴∠G=∠BDG=30°
∵△ADB≌△AEC
∴BD=CE,∠ADB=∠AEC=90°
∴∠GEC=∠AEC﹣∠AED=30°
∴∠G=∠GEC=30°
∴GC=CE
∴CG=BD,且∠BDG=∠G, ∠BFD=∠GFC
∴△BFD≌△CFG(AAS)
∴BF=FC
∴点F是BC中点
(3)如图,连接AF,
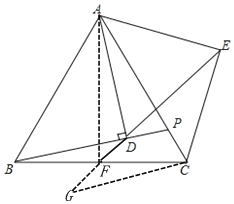
∵△ABC是等边三角形,BF=FC
∴AF⊥BC
∴∠AFC=90°
∴∠AFC=∠AEC=90°
∴点A,点F,点C,点E四点在以AC为直径的圆上
∴EF最大为直径,
即最大值为1


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】综合与实践:
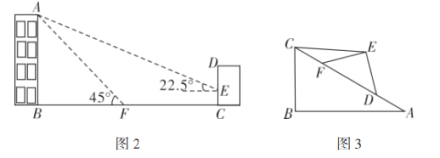
阅读理解:数学兴趣小组在探究如何求![]() 的值,经过思考、讨论、交流,得到以下思路:
的值,经过思考、讨论、交流,得到以下思路:
如图1,作![]() ,使
,使![]() ,
,![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() .
.
设![]() ,则
,则![]() ,
,![]() .
.![]()
![]() .
.
请解决下列问题:
(1)类比求解:求出![]() 的值;
的值;
(2)问题解决:如图2,某住宅楼![]() 的后面有一建筑物
的后面有一建筑物![]() ,当光线与地面的夹角是
,当光线与地面的夹角是![]() 时,住宅在建筑物的墙上留下高
时,住宅在建筑物的墙上留下高![]() 的影子
的影子![]() ;而当光线与地面的夹角是
;而当光线与地面的夹角是![]() 时,住宅楼顶
时,住宅楼顶![]() 在地面上的影子
在地面上的影子![]() 与墙角
与墙角![]() 有
有![]() 的距离(
的距离(![]() ,
,![]() ,
,![]() 在一条直线上).求住宅楼
在一条直线上).求住宅楼![]() 的高度(结果保留根号);
的高度(结果保留根号);
(3)探究发现:如图3,小明用硬纸片做了两个直角三角形,在![]() 中,
中,![]() ,
,![]() ,
,![]() ;在
;在![]() 中,
中,![]() ,
,![]() ,
,![]() .他将
.他将![]() 的斜边
的斜边![]() 与
与![]() 的斜边
的斜边![]() 重合在一起,并将
重合在一起,并将![]() 沿
沿![]() 方向移动.在移动过程中,
方向移动.在移动过程中,![]() ,
,![]() 两点始终在
两点始终在![]() 边上(移动开始时点
边上(移动开始时点![]() 与点
与点![]() 重合).探究在
重合).探究在![]() 移动过程中,是否存在某个位置,使得
移动过程中,是否存在某个位置,使得![]() ?如果存在,直接写出
?如果存在,直接写出![]() 的长度;如果不存在,请说明理由.
的长度;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两地之间有一座山,汽车原来从A地到B地经过C地沿折线A→C→B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10千米,∠A=30°,∠B=45°.则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个自然数从高位到个位是由一个数字或几个数字重复出现组成的,那么我们把这样的自然数叫做循环数,重复的一个或几个数字称为“循环节”,我们把“循环节”的数字个数叫做循环节的阶数.例如:525252,它由“52”依次重复出现组成,所以525252是循环数,它是2阶6位循环数.再如:77,是1阶2位循环数,135135135是3阶9位循环数.
(1)请直接写出1个2阶4位循环数 ,并证明对于任意一个2阶4位循环数,若交换其循环节的数字得到一个新的4位数,则该新数和原数的差能够被9整除.
(2)已知一个能被9整除的2阶4位数.设循环节为ab,且满足a﹣2b为非负偶数,求这个4位循环数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=(m﹣2)x2+2mx+m+3与x轴有两个交点.
(1)求m的取值范围;
(2)当m取满足条件的最大整数时,求抛物线与x轴有两个交点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数
的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数![]() 的图象经过该二次函数图象上点
的图象经过该二次函数图象上点![]() 及点B.
及点B.
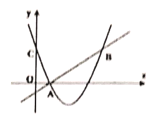
(1)求B点坐标与二次函数的解析式;
(2)根据图象,写出满足![]() 的x的取值范围.
的x的取值范围.
(3)求线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的对称轴为
的对称轴为![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,其部分图像如图所示,则下列结论:①点
之间,其部分图像如图所示,则下列结论:①点![]() ,
,![]() ,
,![]() 是该抛物线上的点,则
是该抛物线上的点,则![]() ;②
;②![]() ;③
;③![]() (
(![]() 为任意实数).其中正确结论的个数是( )
为任意实数).其中正确结论的个数是( )
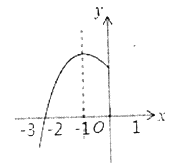
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
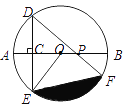
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若DE=![]() ,∠DPA=45°.
,∠DPA=45°.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com