
【题目】
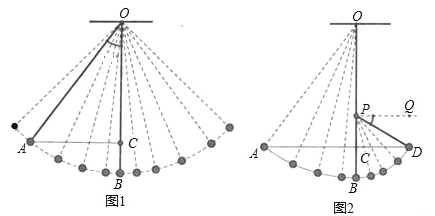
(1)如图1,一条细绳系着一个小球在平面内摆动,已知细绳从悬挂点O到球心的长度为50厘米,小球在带你B位置时达到最低点,当小球在左侧点A时与最低点B时细绳相应所成的角度∠AOB=37°.求点A与点B的高度差BC的值.
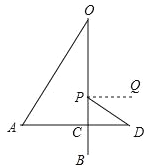
(2)如图2,若在点O的正下方有一个阻碍物P,当小球从左往右落到最低处后,运动轨迹改变,变为以P为圆心,PB为半径继续向右摆动,当摆动至与点A在同一水平高度的点D时,满足PD部分细绳与水平线的夹角∠DPQ=30°,求OP的长度.
【答案】(1)A,B之间的高度差BC为10cm
(2)OP这段细绳的长度为30cm
【解析】
试题分析:(1)根据题意得出CB=OB﹣OC=OB﹣OAcos37°,进而得出答案;
(2)根据题意得出BP=BP﹣CP=PD﹣PDcos60°=10,进而得出PB的长,进而得出答案.
试题解析:(1)∵AD⊥OB,
由题意可得:∠AOB=37°,
则CB=OB﹣OC=OB﹣OAcos37°=50﹣50×0.8=10(cm),
故A,B之间的高度差BC为10cm;
(2)由(1)知,B,D的高度差也是10cm,
故BP=BP﹣CP=PD﹣PDcos60°=10(cm),
解得:PB=20,
则OP=OB﹣BC=50﹣20=30(cm).
答:OP这段细绳的长度为30cm.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程x2﹣8x﹣11=0时,下列变形正确的是( )
A. (x﹣4)2=5 B. (x+4)2=5 C. (x﹣4)2=27 D. (x+4)2=27
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为r,点O到直线l的距离为d,且|d﹣3|+(6﹣2r)2=0,则直线l与⊙O的位置关系是_____.(填“相切、相交、相离”中的一种)
查看答案和解析>>
科目:初中数学 来源: 题型:
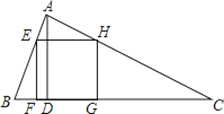
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AC、BD相交于O,能判定这个四边形是正方形的是( )
A. AO=BO=CO=DO,AC⊥BD B. AB∥CD,AC=BD
C. AO=BO,∠A=∠C D. AO=CO,BO=DO,AB=BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com