
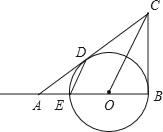
【题目】如图所示,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D.
(1)求证:DE∥OC;
(2)若AD=2,DC=3,且AD2=AEAB,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)首先连接OD,由在△ABC中,∠B=90°,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,易证得Rt△ODC≌Rt△OBC(HL),然后由等腰三角形与三角形外角的性质,证得∠OED=∠BOC,继而证得DE∥OC;
(2)由AD、DC的长可得AC、BC的长,再根据勾股定理即可得AB的长,再根据AD2=AEAB,从而可得AE的长,继而得到OB的长,问题得以解答.
试题解析:(1)连接OD,
∵AC切⊙O点D,∴OD⊥AC,∴∠ODC=∠B=90°,
在Rt△OCD和Rt△OCB中,![]() ,∴Rt△ODC≌Rt△OBC(HL),
,∴Rt△ODC≌Rt△OBC(HL),
∴∠DOC=∠BOC,
∵OD=OE,∴∠ODE=∠OED,
∵∠DOB=∠ODE+∠OED,∴∠BOC=∠OED,∴DE∥OC;
(2)由AD=2,DC=3得:BC=3,AC=5,由勾股定理得AB=![]() =4,
=4,
又∵AD2=AE·AB,∴AE=1,
∴BE=3,OB=![]() BE=
BE=![]() ,∴
,∴![]() =
=![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
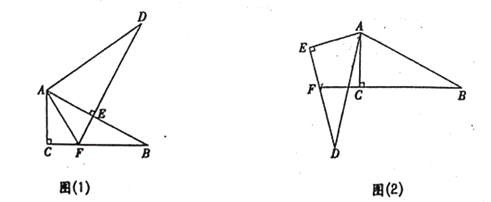
【题目】已知![]() ,其中
,其中![]()
(1)观察发现:将这两个三角形按图(1)所示的方式摆放,使点![]() 落在
落在![]() 上,
上,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,连结
,连结![]() ,易证
,易证![]() ,请你直接写出
,请你直接写出![]() 与
与![]() 之间的数量关系:
之间的数量关系:
(2)类比探究:将![]() 绕点
绕点![]() 旋转到图(2)的位置时,使
旋转到图(2)的位置时,使![]() 交
交![]() 的延长线于点
的延长线于点![]() ,则(1)中的结论还成立吗?若成立,加以证明;若不成立,写出此时
,则(1)中的结论还成立吗?若成立,加以证明;若不成立,写出此时![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
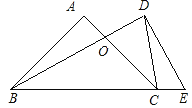
【题目】将一副直角三角板如图摆放,等腰直角三角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同,且斜边BC与BE在同一直线上,AC与BD交于点O,连接CD.
求证:△CDO是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C、D两点在半圆上,CE⊥AB于E,DF⊥AB于F,点P是AB上的一个动点,已知AB=10,CE=4,DF=3,则PC+PD的最小值是( )
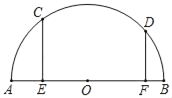
A. 7 B. 7![]() C. 10 D. 8
C. 10 D. 8![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
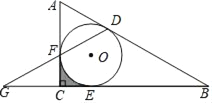
【题目】如图,△ABC中,∠ACB=90°,⊙O是△ABC的内切圆,切点分别为D、E、F.连接DF并延长交BC的延长线于点G.
(1)求证:AF=GC;
(2)若BD=6,AD=4,求⊙O的半径;
(3)在(2)的条件下,求图中由弧EF与线段CF、CE围成的阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点D在![]() 的AB边上,且
的AB边上,且![]() .
.
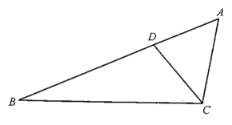
(1)作![]() 的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);
的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,判断直线DE与直线AC的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC 绕点 B 逆时针旋转 30°时,点 C 转到 C′的位置,且BC′与 AC 交于点 D,则 的值为( )
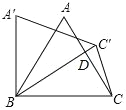
A. 2 ![]() B. 2﹣
B. 2﹣![]() C.
C. ![]() ﹣2 D.
﹣2 D. ![]() ﹣3
﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,某车行经营的A型车去年2月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年2月份与去年2月份卖出的A型车数量相同,则今年2月份A型车销售总额将比去年2月份销售总额增加25%.
(1)求今年2月份A型车每辆销售价多少元?
(2)该车行计划今年3月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的2倍,A.B两种型号车的进货和销售价格如表,问应如何进货才能使这批车获利最多?
A型车 | B型车 | |
进货价格(元/辆) | 1100 | 1400 |
销售价格(元/辆) | 今年的销售价格 | 2400 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com