
【题目】已知![]() ,点
,点![]() 为平面内一点,连接
为平面内一点,连接![]() .
.
(1)探究:
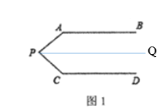
如图1:![]() ,
,![]() ,则
,则![]() 的度数是___________;
的度数是___________;
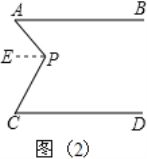
如图2:![]() ,
,![]() ,则
,则![]() 的度数是___________.
的度数是___________.
(2)在图2中试探究![]() ,
,![]() ,
,![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)拓展探究:当点![]() 在直线
在直线![]() ,
,![]() 外,如图3、4所示的位置时,请分别直接写出
外,如图3、4所示的位置时,请分别直接写出![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.

【答案】(1)![]() ;
;![]() .(2)
.(2)![]() 理由见解析;(3)图3.
理由见解析;(3)图3.![]() ,图4.
,图4.![]() .
.
【解析】
(1)①过点P作PQ∥AB,再根据两直线平行,同旁内角互补进行求解;
②过点![]() 作
作![]() ,根据两直线平行,内错角相等进行求解;
,根据两直线平行,内错角相等进行求解;
(2)过点![]() 作
作![]() ,方法同②,把角度换成字母即可求解证明;
,方法同②,把角度换成字母即可求解证明;
(3)根据平行线的性质及三角形的外角定理即可求解.
解:(1)①过点P作PQ∥AB,则PQ∥AB∥CD,
∵![]() ,
,![]() ,
,
∴∠APQ=180°-![]() =35°,
=35°,
∠CPQ=180°-![]() =45°,
=45°,
∴∠APC=∠APQ+∠CPQ=80°
②过点![]() 作
作![]() ,则PE∥AB∥CD,
,则PE∥AB∥CD,
∵![]() ,
,![]() ,
,
∴∠APE=![]() ,∠CPE=
,∠CPE=![]() ,
,
∴![]() =105°
=105°
(2)![]() .
.
理由:如图2.,过点![]() 作
作![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;

3.图3:∵AB∥CD
∴∠![]() =∠PEB-∠PAB=
=∠PEB-∠PAB=![]()
即![]() ,
,
图4. ∵AB∥CD
∴∠![]() =∠PFD-∠PCD=
=∠PFD-∠PCD=![]()
即![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
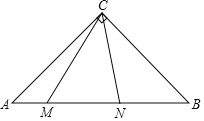
【题目】如图,在Rt△ABC中,∠ACB=90°,CA=CB,M,N分别AB上的两动点,且∠MCN=45°,下列结论:①![]() ;②CM2﹣CN2=NBNA﹣MBMA;③AM2+BN2=MN2;④S△CAM+S△CBN=S△CMN,其中正确的有( )
;②CM2﹣CN2=NBNA﹣MBMA;③AM2+BN2=MN2;④S△CAM+S△CBN=S△CMN,其中正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雅安地震发生后,全国人民抗震救灾,众志成城,值地震发生一周年之际,某地政府又筹集了重建家园的必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)全部物资可用甲型车8辆,乙型车5辆,丙型车 辆来运送.
(2)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(3)为了节省运费,该地政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC的角平分线BD,CE相交于点P.
(1)如果∠A=80,求∠BPC= .
(2)如图②,过点P作直线MN∥BC,分别交AB和AC于点M和N,试求∠MPB+∠NPC的度数(用含∠A的代数式表示) .
(3)将直线MN绕点P旋转。
(i)当直线MN与AB,AC的交点仍分别在线段AB和AC上时,如图③,试探索∠MPB,∠NPC,∠A三者之间的数量关系,并说明你的理由。
(ii)当直线MN与AB的交点仍在线段AB上,而与AC的交点在AC的延长线上时,如图④,试问(i)中∠MPB,∠NPC,∠A三者之间的数量关系是否仍然成立?若成立,请说明你的理由;若不成立,请给出∠MPB,∠NPC,∠A三者之间的数量关系,并说明你的理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1 , 它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,它交x轴于A2;将C2绕A2旋转180°得到C3 , 交x轴于A3;…如此进行下去,直至得到C7 , 若点P(13,m)在第7段抛物线C7上,则m= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践操作:如图,在 ![]() 中,∠ABC=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法):
中,∠ABC=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法):
(1)作∠BCA的角平分线,交AB于点O;
(2)以O为圆心,OB为半径作圆.
综合运用:在你所作的图中,
(3)AC与⊙O的位置关系是(直接写出答案);
(4)若BC=6,AB=8,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)图1阴影面积可表示为_______,图2阴影面积可表示为_____.
请利用图形面积的不同表示方法,写出一个关于![]() 、
、![]() 的恒等式_______.
的恒等式_______.
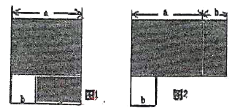
(2)如图所示的长方形或正方形三类卡片各有若干张,请你用这些卡片,拼成一个长方形或正方形图形。验证公式(a+b)2=a2+2ab+b2.

(3)图![]() 是一个长为2m、宽为2m的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图
是一个长为2m、宽为2m的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图![]() 的形状拼成一个正方形。
的形状拼成一个正方形。

请用两种不同的方法求图![]() 中阴影部分的面积:
中阴影部分的面积:
方法1:___________________;
方法2:__________________;
观察图![]() 写出下列三个代数式之间的等量关系:
写出下列三个代数式之间的等量关系:
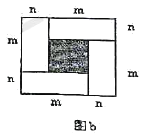
![]() ,
,![]() ,
,![]()
_____________________________;
(4)根据(3)题中的等量关系,解决如下问题:
若![]() ,
,![]() ,则
,则![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄冈市三运会期间,武穴黄商有一种姚明牌运动装每件的销售价y(元)与时间x(周)之间的函数关系式对应的点都在如图所示的图象上,该图象从左至右,依次是线段AB、线段BC、线段CD,而这种运动装每件的进价Z(元)与时间x(周)之间的函数关系式为Z= ![]() (1≤x≤16且x为整数)
(1≤x≤16且x为整数)
(1)写出每件的销售价y(元)与时间x(周)之间的函数关系式;
(2)设每件运动装销售利润为w,写出w(元)与时间x(周)之间的函数关系式;
(3)求该运动装第几周出销时,每件运动装的销售利润最大?最大利润为多少?(6分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com