
【题目】如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.
(1)ΔABE与ΔADF相似吗?请说明理由.
(2)若AB=6,AD=12,BE=8,求FD的长.

【答案】(1)、相似,证明过程见解析;(2)、FD=7.2
【解析】
试题分析:(1)、首先根据矩形和DF⊥AE可得∠B=∠AFD,根据AD∥BC可得∠DAF=∠AEB,从而得出三角形相似;(2)、首先根据Rt△ABE的勾股定理求出AE的长度,然后根据三角形相似得出DF的长度.
试题解析:(1)、∵ABCD为矩形 ∴∠BAD=∠B=90° ∵DF⊥AE ∴∠AFD=90°
∵AD∥BC ∴∠DAF=∠AEB 在△ABE和△AFD中 ∠B=∠AFD,∠DAF=∠AEB ∴△ABE∽△ADF
(2)、∵AB=6,BE=8,∠B=90° ∴AE=10 ∵△ABE∽△ADF ∴![]()
∴![]() ∴DF=7.2
∴DF=7.2


科目:初中数学 来源: 题型:
【题目】某校为了丰富校园文化,举行初中生书法大赛,决赛设置了7个获奖名额,共有13名选手进入决赛,选手决赛得分均不相同,小颖知道自己的比赛分数后,要判断自己能否获奖,需要知道这13名同学成绩的( )
A.众数B.中位数C.平均数D.方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2)
(1)写出点A、B的坐标:A( , )、B( , )
(2)将△ABC先向左平移1个单位长度,再向上平移2个单位长度,得到△A′B′C′,画出△A′B′C′
(3)写出三个顶点坐标A′( 、 )、B′( 、 )、C′ ( 、 )
(4)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题: 小明和同学去公园春游.在公园门口看到公园的公告如图.
(1)如果小明他们共19人,那么他们买19张5元的门票省钱,还是买1张20人的团体票省钱?请说明理由.
(2)如果小明他们买1张20人的团体票,比每人买1张5元的门票总共少花了10元,你能求出小明他们共有多少人吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
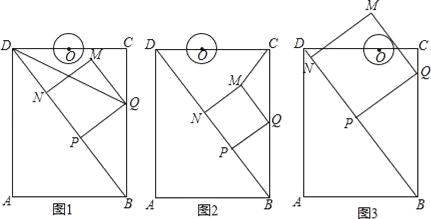
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3m/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单位:s)(0<t<![]() ).
).
(1)如图1,连接DQ平分∠BDC时,t的值为 ;
(2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值;
(3)请你继续进行探究,并解答下列问题:
①证明:在运动过程中,点O始终在QM所在直线的左侧;
②如图3,在运动过程中,当QM与⊙O相切时,求t的值;并判断此时PM与⊙O是否也相切?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com