
分析 实数的分类:$\left\{\begin{array}{l}{有理数\left\{\begin{array}{l}{正有理数}\\{0}\\{负有理数}\end{array}\right.}\\{无理数\left\{\begin{array}{l}{正无理数}\\{负无理数}\end{array}\right.}\end{array}\right.$,依此即可求解.
解答 解:有理数集合 0,-2,0.12,-$\root{3}{\frac{8}{27}}$,$\sqrt{4}$,$\frac{22}{7}$,1.21212121…;
无理数集合 $\sqrt{3}$,$\sqrt{8}$,-$\sqrt{27}$,$\frac{\sqrt{3}}{2}$,0.1010010001…(相邻两个1之间0的个数逐次加1),$\frac{π}{4}$;
正数集合 $\sqrt{3}$,$\sqrt{8}$,0.12,$\sqrt{4}$,$\frac{22}{7}$,$\frac{\sqrt{3}}{2}$,1.21212121…,0.1010010001…(相邻两个1之间0的个数逐次加1),$\frac{π}{4}$;
整数集合 0,-2,$\sqrt{4}$;
非负数集合 0,$\sqrt{3}$,$\sqrt{8}$,0.12,$\sqrt{4}$,$\frac{22}{7}$,$\frac{\sqrt{3}}{2}$,1.21212121…,0.1010010001…(相邻两个1之间0的个数逐次加1),$\frac{π}{4}$;
分数集合 0.12,-$\root{3}{\frac{8}{27}}$,$\frac{22}{7}$,1.21212121….
故答案为:0,-2,0.12,-$\root{3}{\frac{8}{27}}$,$\sqrt{4}$,$\frac{22}{7}$,1.21212121…;$\sqrt{3}$,$\sqrt{8}$,-$\sqrt{27}$,$\frac{\sqrt{3}}{2}$,0.1010010001…(相邻两个1之间0的个数逐次加1),$\frac{π}{4}$;$\sqrt{3}$,$\sqrt{8}$,0.12,$\sqrt{4}$,$\frac{22}{7}$,$\frac{\sqrt{3}}{2}$,1.21212121…,0.1010010001…(相邻两个1之间0的个数逐次加1),$\frac{π}{4}$;0,-2,$\sqrt{4}$,;0,$\sqrt{3}$,$\sqrt{8}$,0.12,$\sqrt{4}$,$\frac{22}{7}$,$\frac{\sqrt{3}}{2}$,1.21212121…,0.1010010001…(相邻两个1之间0的个数逐次加1),$\frac{π}{4}$;0.12,-$\root{3}{\frac{8}{27}}$,$\frac{22}{7}$,1.21212121….
点评 本题主要考查了实数的定义,要求掌握实数的范围以及分类方法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
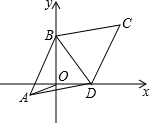 如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是5$\sqrt{3}$-5.
如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是5$\sqrt{3}$-5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com