

���� ��1�����ô���ϵ��������κ����Ľ���ʽ��
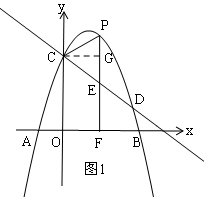
��2���Ȱ�C�����ֱ��CD�����m��ֵ����ʾP��m��-m2+2m+3����E��m��-$\frac{3}{4}$m+3����
����CPE����CEΪ���ĵ���������ʱ�������������
�ٵ�CE=CPʱ����C��CG��PF��G������OC=FG�з��̽�����ɣ�
�ڵ�CE=PEʱ���ȱ�ʾCE��EG��CG�ij������ù��ɶ����ã�CG2+EG2=CE2���з��̽�����ɣ�
��3���ȸ��ݵ�P���������ϣ�G��ֱ��y=x����P��m��-m2+2m+3����G��a��a����
��ͼ3���������ߣ������������������Σ�֤����PHG�ס�BNP����$\frac{PN}{GH}$=$\frac{BN}{PH}$=$\frac{PB}{PG}$������ֱ�DZ߱�Ϊ1��2�з�������������m��
��ͼ4��ͬ���з�������m��ֵ��
���  �⣺��1����A��-1��0����C��0��3������������y=-x2+bx+c�еã�
�⣺��1����A��-1��0����C��0��3������������y=-x2+bx+c�еã�
$\left\{\begin{array}{l}{-1-b+c=0}\\{c=3}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$��
�������ߵĽ���ʽΪ��y=-x2+2x+3��
��2����C��0��3������ֱ��y=-$\frac{3}{4}$x+m�ã�
m=3��
��ֱ�ߵĽ���ʽΪ��y=-$\frac{3}{4}$x+3��
��P��m��-m2+2m+3����E��m��-$\frac{3}{4}$m+3����
�ٵ�CE=CPʱ����C��CG��PF��G��
��PE=��-m2+2m+3��-��-$\frac{3}{4}$x+3��=-m2+$\frac{11}{4}$m��
��PC=CE��CG��PF��
��PG=EG��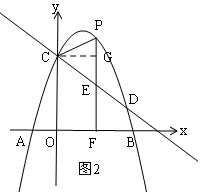
��EG=$\frac{1}{2}$PE=$\frac{-4{m}^{2}+11m}{8}$��
��OC=FG=EF+EG��
��-$\frac{3}{4}$m+3+$\frac{-4{m}^{2}+11m}{8}$=3��
��ã�m1=0��m2=$\frac{5}{4}$��
��m=$\frac{5}{4}$ʱ��y=-m2+2m+3=-��$\frac{5}{4}$��2+2��$\frac{5}{4}$+3=$\frac{63}{16}$��
��P��$\frac{5}{4}$��$\frac{63}{16}$����
�ڵ�CE=PEʱ��
��Rt��CEG��CG=m��EG=FG-EF=3-��-$\frac{3}{4}m$+3��=$\frac{3}{4}$m��
CE=PE=-m2+$\frac{11}{4}m$��
�ɹ��ɶ����ã�CG2+EG2=CE2��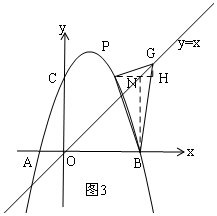
��-m2+$\frac{11}{4}m$��2=m2+��$\frac{3}{4}m$��2��
��ã�m1=4���ᣩ��m2=$\frac{3}{2}$��
��m=$\frac{3}{2}$ʱ��y=-$\frac{9}{4}$+2��$\frac{3}{2}$+3=$\frac{15}{4}$��
��P��$\frac{3}{2}$��$\frac{15}{4}$����
��������������CPE����CEΪ���ĵ���������ʱ����P�������ǣ�$\frac{5}{4}$��$\frac{63}{16}$����$\frac{3}{2}$��$\frac{15}{4}$����
��3����P��m��-m2+2m+3����G��a��a����
��ͼ3����B��BN��y�ᣬ��P��PH��x�ᣬ����N����G��GH��PN������ΪH�����PHG=��BNP=90�㣬
���NBP+��BPN=90�㣬
�ߡ�BPG=90�㣬
���BPN+��NPG=90�㣬
���NBP=��NPG��
���PHG�ס�BNP��
��$\frac{PN}{GH}$=$\frac{BN}{PH}$=$\frac{PB}{PG}$��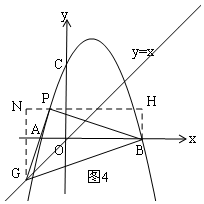
��$\frac{PB}{PG}$=2��
��$\frac{PN}{GH}=\frac{BN}{PH}$=2��
��$\frac{3-m}{a+{m}^{2}-2m-3}$=$\frac{-{m}^{2}+2m+3}{a-m}$=2��
��$\left\{\begin{array}{l}{2a+2{m}^{2}-4m-6=3-m}\\{-{m}^{2}+2m+3=2a-2m}\end{array}\right.$��
��ã�m1=-3��m2=2��
��ͼ4����P��NH��x�ᣬ��G��GN��NH����B��BH��NH������ֱ�ΪN��H��
ͬ���ã���PNG�ס�BHP��
��$\frac{PN}{BH}$=$\frac{NG}{PH}$=$\frac{PG}{PB}$=$\frac{1}{2}$��
��$\frac{-a+m}{-{m}^{2}+2m+3}$=$\frac{-a-{m}^{2}+2m+3}{3-m}$=$\frac{1}{2}$��
��$\left\{\begin{array}{l}{-2a+2m=-{m}^{2}+2m+3}\\{-2a-2{m}^{2}+4m+6=3-m}\end{array}\right.$��
��ã�m=$\frac{5��\sqrt{97}}{6}$��
������������Ӧ��P�ĺ�����Ϊ-3��2��$\frac{5+\sqrt{97}}{6}$��$\frac{5-\sqrt{97}}{6}$��
���� �����Ƕ��κ������ۺ�Ӧ�ã����������ô���ϵ���������ʽ���������˶��κ��������ʡ����������ε����ʺ��ж���ע����ݽ���ʽ��ʾ������꣬���ɵ�������ʾ�߶εij������õ�����ϵ�з��̻�����⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2-6x+9 | B�� | 1+x2 | C�� | x+2xy+1 | D�� | x2+2x-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
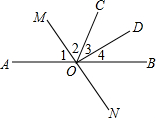 ��ͼ��ֱ��AB��MN�ཻ�ڵ�O��ODƽ�֡�MON����1=��2�����жϡ�3���4֮��Ĺ�ϵ����˵�����ɣ�
��ͼ��ֱ��AB��MN�ཻ�ڵ�O��ODƽ�֡�MON����1=��2�����жϡ�3���4֮��Ĺ�ϵ����˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3 | B�� | 3 | C�� | -4 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com