
 如图,在△ABC中,点E,F在BC上,EM垂直平分AB交AB于点M,FN垂直平分AC交AC于点N,∠EAF=90°,BC=12,EF=5.
如图,在△ABC中,点E,F在BC上,EM垂直平分AB交AB于点M,FN垂直平分AC交AC于点N,∠EAF=90°,BC=12,EF=5.分析 (1)先根据线段垂直平分线的性质得出∠B=∠BAE,∠C=∠CAF,再由三角形内角和定理得出∠BEA+∠CAF=45°,由∠BAC=∠BEA+∠EAF+∠CAF即可得出结论;
(2)先根据线段垂直平分线的性质得出EB=EA,FA=FC,根据EA•FA的值即可得出结论.
解答 解:(1)∵EM垂直平分AB,
∴∠B=∠BAE.
∵FN垂直平分AC,
∴∠C=∠CAF.
∵∠B+∠BAE+∠EAF+∠C+∠CAF=180°,∠EAF=90°,
∴2∠BEA+2∠CAF=90°,
∴∠BEA+∠CAF=45°,
∴∠BAC=∠BEA+∠EAF+∠CAF=45°+90°=135°;
(2)∵EM垂直平分AB,
∴EB=EA.
∵FN垂直平分AC,
∴FA=FC.
∵BC=12,EF=5,
∴EA+FA=12-5=7.
∵EF=5,∠EAF=90°,
∴EA2+FA2=(EA+FA)2-2EA•FA=EF2=25,
∴$\frac{1}{2}$EA•FA=6,
∴S△EAF=6.
点评 本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:解答题
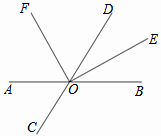 如图,已知直线AB与CD相交于点O,OE是∠BOD的平分线,OF是∠AOD的平分线.
如图,已知直线AB与CD相交于点O,OE是∠BOD的平分线,OF是∠AOD的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
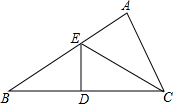 如图,已知△ABC,AB=10,BC边的垂直平分线交AB、BC于点E、D,AC=6,则△ACE的周长是( )
如图,已知△ABC,AB=10,BC边的垂直平分线交AB、BC于点E、D,AC=6,则△ACE的周长是( )| A. | 13 | B. | 16 | C. | 11 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 内错角相等 | B. | 如果$\frac{x-5}{2}=\frac{3-x}{3}$,那么x=4 | ||
| C. | 一个角的补角大于这个角 | D. | 同位角相等,两直线平行 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 六年级上册数学课本共有158页 | B. | 某同学的体重约是67千克 | ||
| C. | 1纳米等于1毫米的一百万分之一 | D. | 小明收集了9片树叶 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将一张长方形纸片ABCD沿EF折叠,点D、C分别落在点D′、C′处,若∠1=56°,则∠DEF的度数是( )
如图,将一张长方形纸片ABCD沿EF折叠,点D、C分别落在点D′、C′处,若∠1=56°,则∠DEF的度数是( )| A. | 56° | B. | 62° | C. | 68° | D. | 124° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com