
【题目】将一块长为a米的长方形苗圃划分成8个部分(如图),其中A,B,C三块苗圃是正方形,边长为b 米,苗圃H也是正方形.
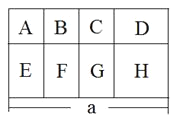
(1)求整个苗圃的面积;
(2)若A,B,C三个苗圃种甲种花卉,每平方米利润250元,D,H两个苗圃种乙种花卉,每平方米利润120元,E,F,G三个苗圃种丙种花卉,每平方米利润100元,请问整个苗圃的利润为多少元?(结果用代数式表示,要化简)
【答案】(1) a2-2ab;(2) 570b2+120a2-300ab
【解析】
(1)根据长方形苗圃的长为a米,A,B,C三块正方形苗圃的边长为b 米,可得出正方形苗圃H的边长为![]() ,进而可得出D的长和宽以及E、F、G所组成的长方形的长和宽,再根据长方形和正方形的面积公式即可得出答案;
,进而可得出D的长和宽以及E、F、G所组成的长方形的长和宽,再根据长方形和正方形的面积公式即可得出答案;
(2)分别求出A,B,C的面积之和,D、H的面积之和以及E、F、G的面积之和,再分别乘以各自的每平方米利润,即可得出答案.
(1)S=(a-3b+b)a=a2-2ab;
(2)250×3b2+120(a-3b)(a-3b+b)+100×3b(a-3b)
=750b2+120a2-600ab+720b2+300ab-900b2,
=570b2+120a2-300ab.


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象经过点
的图象经过点![]() ,与
,与![]() 轴分别交于点
轴分别交于点![]() ,点
,点![]() .点
.点![]() 是直线
是直线![]() 上方的抛物线上一动点.
上方的抛物线上一动点.
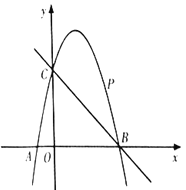
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接![]() ,
,![]() ,并把
,并把![]() 沿
沿![]() 轴翻折,得到四边形
轴翻折,得到四边形![]() .若四边形
.若四边形![]() 为菱形,请求出此时点
为菱形,请求出此时点![]() 的坐标;
的坐标;
(3)当点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 的面积最大?求出此时
的面积最大?求出此时![]() 点的坐标和四边形
点的坐标和四边形![]() 的最大面积.
的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
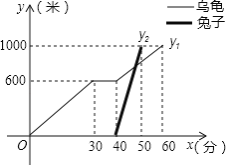
①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 .(把你认为正确说法的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
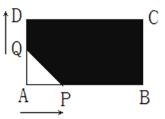
【题目】如图,长方形ABCD的边长分别为AB=12cm,AD=8cm,点P、Q从点A出发,P沿线段AB运动,点Q沿线段AD运动(其中一点停止运动,另一点也随着停止),设AP=AQ=xcm在这个变化过程中,图中阴影部分的面积y(cm2)也随之变化.
(1)写出y与x的关系式
(2)当AP由2cm变到8cm,图中阴影部分的面积y是如何变化的?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图a是一个长为2m、宽为2n的长方形,沿图中实现用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.

(1)图b中,大正方形的边长是 .阴影部分小正方形的边长是 ;
(2)观察图b,写出(m+n)2,(m﹣n)2,mn之间的一个等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车行驶时的耗油量为0.1升/千米,如图是油箱剩余油量![]() (升)关于加满油后已行驶的路程
(升)关于加满油后已行驶的路程![]() (千米)的函数图象.
(千米)的函数图象.

(1)根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;
(2)求![]() 关于
关于![]() 的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com