
【题目】如图,已知二次函数![]() 的图象经过点
的图象经过点![]() ,与
,与![]() 轴分别交于点
轴分别交于点![]() ,点
,点![]() .点
.点![]() 是直线
是直线![]() 上方的抛物线上一动点.
上方的抛物线上一动点.
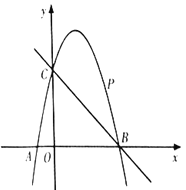
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接![]() ,
,![]() ,并把
,并把![]() 沿
沿![]() 轴翻折,得到四边形
轴翻折,得到四边形![]() .若四边形
.若四边形![]() 为菱形,请求出此时点
为菱形,请求出此时点![]() 的坐标;
的坐标;
(3)当点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 的面积最大?求出此时
的面积最大?求出此时![]() 点的坐标和四边形
点的坐标和四边形![]() 的最大面积.
的最大面积.
【答案】(1)该二次函数的表达式为![]() ;(2)点P的坐标为(
;(2)点P的坐标为(![]() ,
,![]() );(3)P点的坐标为
);(3)P点的坐标为![]() ,四边形ABPC的面积的最大值为
,四边形ABPC的面积的最大值为![]() .
.
【解析】(1)根据待定系数法,可得函数解析式;
(2)根据菱形的对角线互相平分,可得P点的纵坐标,根据函数值与自变量的对应关系,可得答案;
(3)根据面积的和差,可得二次函数,根据二次函数的性质,可得m的值,根据自变量与函数值的对应关系,可得P点坐标.
【解答】(1)将点B和点C的坐标代入![]() ,
,
得 ![]() ,解得
,解得![]() ,
,![]() .
.
∴ 该二次函数的表达式为![]() .
.
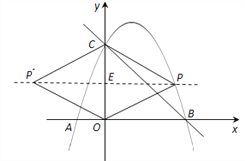
(2)若四边形POP′C是菱形,则点P在线段CO的垂直平分线上;
如图,连接PP′,则PE⊥CO,垂足为E,
∵ C(0,3),
∴ E(0,![]() ),
),
∴ 点P的纵坐标等于![]() .
.
∴ ![]() ,
,
解得![]() ,
,![]() (不合题意,舍去),
(不合题意,舍去),
∴ 点P的坐标为(![]() ,
,![]() ).
).
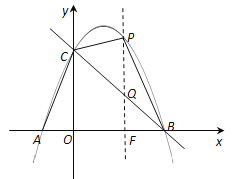
(3)过点P作y轴的平行线与BC交于点Q,与OB交于点F,
设P(m,![]() ),设直线BC的表达式为
),设直线BC的表达式为![]() ,
,
则 ![]() , 解得
, 解得 ![]() .
.
∴直线BC的表达式为 ![]() .
.
∴Q点的坐标为(m,![]() ),
),
∴![]() .
.
当![]() ,
,
解得![]() ,
,
∴ AO=1,AB=4,
∴ S四边形ABPC =S△ABC+S△CPQ+S△BPQ
=![]()
=![]()
=![]() .
.
当![]() 时,四边形ABPC的面积最大.
时,四边形ABPC的面积最大.
此时P点的坐标为![]() ,四边形ABPC的面积的最大值为
,四边形ABPC的面积的最大值为![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
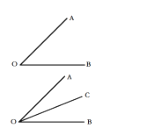
【题目】根据阅读材料,回答问题.
材料:如图所示,有公共端点(O)的两条射线组成的图形叫做角(![]() ).如果一条射线(
).如果一条射线(![]() )把一个角(
)把一个角(![]() )分成两个相等的角(
)分成两个相等的角(![]() 和
和![]() ),这条射线(
),这条射线(![]() )叫做这个角的平分线.这时,
)叫做这个角的平分线.这时,![]() (或
(或![]() ).
).
问题:平面内一定点A在直线![]() 的上方,点O为直线
的上方,点O为直线![]() 上一动点,作射线
上一动点,作射线![]() ,
,![]() ,
,![]() ,当点O在直线
,当点O在直线![]() 上运动时,始终保持
上运动时,始终保持![]() ,
,![]() ,将射线
,将射线![]() 绕点O顺时针旋转60°得到射线
绕点O顺时针旋转60°得到射线![]() .
.
(1)如图1,当点O运动到使点A在射线![]() 的左侧时,若
的左侧时,若![]() 平分
平分![]() ,求
,求![]() 的度数;
的度数;
(2)当点O运动到使点A在射线![]() 的左侧,
的左侧,![]() 时,求
时,求![]() 的值;
的值;
(3)当点O运动到某一时刻时,![]() ,直接写出此时
,直接写出此时![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
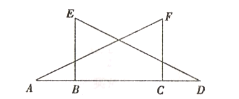
【题目】如图,△ACF≌△DBE,其中点A、B、C、D在一条直线上.
(1)若BE⊥AD,∠F=62°,求∠A的大小.
(2)若AD=9cm,BC=5cm,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=36°,CD是∠ACB的平分线交AB于点D,过点A作AE∥BC,交CD的延长线于点E.
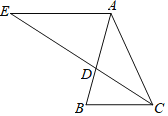
(1)求∠ADC的度数;
(2)求证:AE=AC
(3)试问△ADE是等腰三角形吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.

(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七(1)班的数学兴趣小组在活动中,对“线段中点”问题进行以下探究.已知线段![]() ,点
,点![]() 为
为![]() 上一个动点,点
上一个动点,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.

(1)如图1,若点![]() 在线段
在线段![]() 上,且
上,且![]() ,求
,求![]() 的长度;
的长度;
(2)如图2,若点![]() 是线段
是线段![]() 上任意一点,则
上任意一点,则![]() 的长度为______
的长度为______![]() ;
;
(3)若点![]() 在线段
在线段![]() 的延长线上,其余条件不变,借助图3探究
的延长线上,其余条件不变,借助图3探究![]() 的长度,请直接写出
的长度,请直接写出![]() 的长度(不写探究过程).
的长度(不写探究过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:用2辆A型车和1辆B型车装满货物一次可运货10t;用1辆A型车和2辆B型车装满货物一次可运货11t.某物流公司现有35t货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都装满货物.根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一块长为a米的长方形苗圃划分成8个部分(如图),其中A,B,C三块苗圃是正方形,边长为b 米,苗圃H也是正方形.
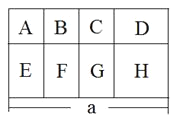
(1)求整个苗圃的面积;
(2)若A,B,C三个苗圃种甲种花卉,每平方米利润250元,D,H两个苗圃种乙种花卉,每平方米利润120元,E,F,G三个苗圃种丙种花卉,每平方米利润100元,请问整个苗圃的利润为多少元?(结果用代数式表示,要化简)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com