
【题目】如图,点E,F在函数y= ![]() 的图象上,直线EF分别与x轴、y轴交于点A、B,且BE:BF=1:3,则△EOF的面积是 .
的图象上,直线EF分别与x轴、y轴交于点A、B,且BE:BF=1:3,则△EOF的面积是 . 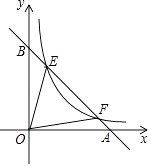
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的盒子,甲盒子中装有3张卡片,卡片上分别写着3cm、7cm、9cm;乙盒子中装有4张卡片,卡片上分别写着2cm、4cm、6cm、8cm;盒子外有一张写着5cm的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
(1)请用树状图或列表的方法求这三条线段能组成三角形的概率;
(2)求这三条线段能组成直角三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
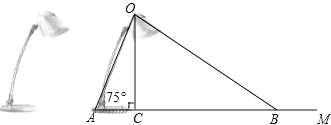
【题目】如图为放置在水平桌面上的台灯的平面示意图,灯臂AO长为40cm,与水平面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,求该台灯照亮水平面的宽度BC(不考虑其他因素,结果精确到0.1cm.温馨提示:sin75°≈0.97,cos75°≈0.26, ![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数之和为m,内部的格点个数为n,试探究S与m、n之间的关系式.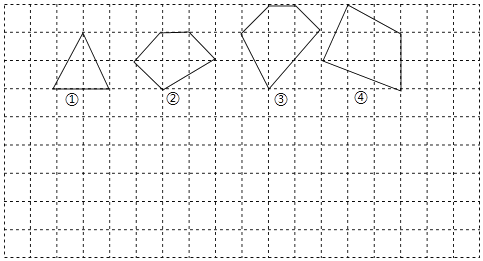
(1)根据图中提供的信息填表:
格点多边形各边上的 | 格点边多边形内部的 | 格点多边形的面积 | |
多边形1 | 4 | 1 | 2 |
多边形2 | 5 | 2 | ② |
多边形3 | 6 | 3 | 5 |
多边形4 | ① | 4 |
|
一般格点多边形 | m | n | S |
则S=(用含m、n的代数式表示)
(2)对正三角形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,如图1、2是该正三角形格点中的两个多边形:设格点多边形的面积为S,该多边形各边上的格点个数之和为m,内部的格点个数为n,试探究S与m、n之间的关系式.则S与m、n之间的关系为S=(用含m、n的代数式表示).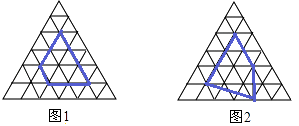
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1计算:![]() ;
;
(2)解不等式组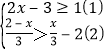
请结合题意填空,完成本题的解答:
解不等式(1),得______________.
解不等式(2),得_______________.
把不等式(1)和(2)的解集在数轴上表示出来
![]()
∴原不等式组的解集为_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A, D1,D三点的坐标分别是(0,4),(0,3),(0,2).

(1)对称中心的坐标;
(2)写出顶点B, C, B1 , C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
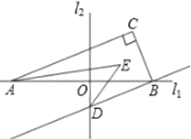
【题目】如图,直线![]() 直线
直线![]() ,垂足为
,垂足为![]() ,
,![]() 如图放置,过点
如图放置,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,在
,在![]() 内取一点
内取一点![]() ,连接
,连接![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,则
,则![]() _______.
_______.
(2)若![]() ,
,![]() ,则
,则![]() _______°.(用含
_______°.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com