
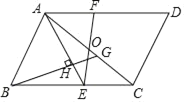
【题目】如图,在平行四边形ABCD中,点O是对角线AC的中点,点E是BC上一点,且AB=AE,连接EO并延长交AD于点F.过点B作AE的垂线,垂足为H,交AC于点G.
(1)若AH=3,HE=1,求△ABE的面积;
(2)若∠ACB=45°,求证:DF=![]() CG.
CG.
【答案】(1)2![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)利用勾股定理即可得出BH的长,进而运用公式得出△ABE的面积;
(2)过A作AM⊥BC于M,交BG于K,过G作GN⊥BC于N,判定△AME≌△BNG(AAS),可得ME=NG,进而得出BE=![]() GC,再判定△AFO≌△CEO(AAS),可得AF=CE,即可得到DF=BE=
GC,再判定△AFO≌△CEO(AAS),可得AF=CE,即可得到DF=BE=![]() CG.
CG.
解:(1)∵AH=3,HE=1,
∴AB=AE=4,
又∵Rt△ABH中,BH=![]() ,
,
∴S△ABE=![]() ;
;
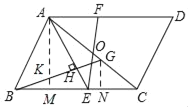
(2)如图,过A作AM⊥BC于M,交BG于K,过G作GN⊥BC于N,则∠AMB=∠AME=∠BNG=90°,
∵∠ACB=45°,
∴∠MAC=∠NGC=45°,
∵AB=AE,
∴BM=EM=![]() BE,∠BAM=∠EAM,
BE,∠BAM=∠EAM,
又∵AE⊥BG,
∴∠AHK=90°=∠BMK,而∠AKH=∠BKM,
∴∠MAE=∠NBG,
设∠BAM=∠MAE=∠NBG=α,则∠BAG=45°+α,∠BGA=∠GCN+∠GBC=45°+α,
∴AB=BG,
∴AE=BG,
在△AME和△BNG中,
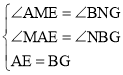 ,
,
∴△AME≌△BNG(AAS),
∴ME=NG,
在等腰Rt△CNG中,NG=NC,
∴GC=![]() NG=
NG=![]() ME=
ME=![]() BE,
BE,
∴BE=![]() GC,
GC,
∵O是AC的中点,
∴OA=OC,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠OAF=∠OCE,∠AFO=∠CEO,
∴△AFO≌△CEO(AAS),
∴AF=CE,
∴AD﹣AF=BC﹣EC,即DF=BE,
∴DF=BE=![]() CG.
CG.


科目:初中数学 来源: 题型:
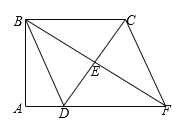
【题目】如图,四边形ABCD中,∠A=∠ABC=90°,E是边CD的中点,连接BE并延长与AD的延长线相交于点F,连接CF.四边形BDFC是平行四边形吗?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
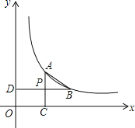
【题目】(1)如图,已知点A、B在双曲线![]() (x>0)上,AC⊥x轴于C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点,点B的横坐标为b.A与B的坐标分别为_____、______(用b与k表示),由此可以猜想AP与CP的数量关系是______.
(x>0)上,AC⊥x轴于C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点,点B的横坐标为b.A与B的坐标分别为_____、______(用b与k表示),由此可以猜想AP与CP的数量关系是______.
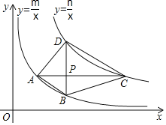
(2)四边形ABCD的四个顶点分别在反比例函数y![]() 与y
与y![]() 的图象上,对角线BD∥y轴,且BD⊥AC于点P,P是BD的中点,点B的横坐标为4.
的图象上,对角线BD∥y轴,且BD⊥AC于点P,P是BD的中点,点B的横坐标为4.
①当![]() 时,判断四边形ABCD的形状并说明理由.
时,判断四边形ABCD的形状并说明理由.
②四边形ABCD能否成为正方形?若能,直接写出此时m,n之间的数量关系;若不能,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
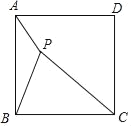
【题目】如图,已知P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP按顺时针方向旋转使点A与点C重合,这时P点旋转到G点.
(1)请画出旋转后的图形,说出此时△ABP以点B为旋转中心最少旋转了多少度;
(2)求出PG的长度;
(3)请你猜想△PGC的形状,并说明理由;
(4)请你计算∠BGC的角度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接“十一”小长假的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:
运动鞋 | 甲 | 乙 |
进价(元/双) | m | m﹣20 |
售价(元/双) | 240 | 160 |
已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于21700元,且不超过22300元,问该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠a(50<a<70)元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】望江中学为了了解学生平均每天“诵读经典”的时间,在全校范围内随机抽查了部分学生进行调查统计,并将调查统计的结果分为:每天诵读时间t≤20分钟的学生记为A类,20分钟<t≤40分钟的学生记为B类,40分钟<t≤60分钟的学生记为C类,t>60分钟的学生记为D类四种.将收集的数据绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
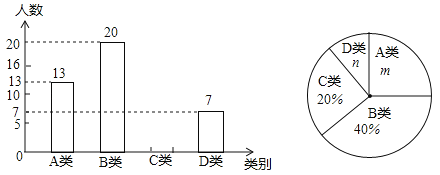
(1)m=%,n=%,这次共抽查了名学生进行调查统计;
(2)请补全上面的条形统计图;
(3)如果该校共有1200名学生,请你估计该校C类学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
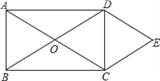
【题目】如图所示,O是矩形ABCD的对角线的交点,作DE∥AC,CE∥BD,DE、CE相交于点E.求证:
(1)四边形OCED是菱形.
(2)连接OE,若AD=4,CD=3,求菱形OCED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
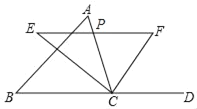
【题目】如图,△ABC中,点P是AC边上一个动点,过P作直线EF∥BC,交∠ACB的平分线于点E,交∠ACB的外角∠ACD平分线于点F.
(1)请说明:PE=PF;
(2)当点P在AC边上运动到何处时,四边形AECF是矩形?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+
x2+![]() x+3
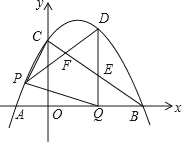
x+3![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).
(1)求直线BC的函数表达式;
(2)①直接写出P,D两点的坐标(用含t的代数式表示,结果需化简)
②在点P、Q运动的过程中,当PQ=PD时,求t的值;
(3)试探究在点P,Q运动的过程中,是否存在某一时刻,使得点F为PD的中点?若存在,请直接写出此时t的值与点F的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com