
【题目】如图,抛物线y=﹣![]() x2+
x2+![]() x+3
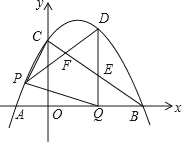
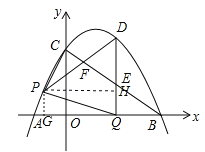
x+3![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).
(1)求直线BC的函数表达式;
(2)①直接写出P,D两点的坐标(用含t的代数式表示,结果需化简)
②在点P、Q运动的过程中,当PQ=PD时,求t的值;
(3)试探究在点P,Q运动的过程中,是否存在某一时刻,使得点F为PD的中点?若存在,请直接写出此时t的值与点F的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x+3
x+3![]() ;(2)①P(
;(2)①P(![]() t﹣3,
t﹣3,![]() t),D(9﹣2t,﹣
t),D(9﹣2t,﹣![]() t2+
t2+![]() t),②
t),②![]() ;(3)t=3,F(
;(3)t=3,F(![]() ,
,![]() ).
).
【解析】试题分析:(1)先求出B、C两点的坐标,进而求出直线BC的函数表达式;
(2)①过点P作PG⊥x轴于点G ,由AO=3,BO=9,OC=![]() ,得到∠CAO=60°,∠APG=30°,从而有AP=t, AG=
,得到∠CAO=60°,∠APG=30°,从而有AP=t, AG=![]() ,PG=
,PG=![]() ,得到P的坐标.由OQ=
,得到P的坐标.由OQ=![]() ,得到D的横坐标,由D在抛物线上,得到D的纵坐标;
,得到D的横坐标,由D在抛物线上,得到D的纵坐标;
②过点P作PG⊥x轴于点G,PH⊥QD于点H,得到四边形PGQH是矩形,从而有QD=2HQ=2PG,解关于t的方程即可;
(3)由中点坐标公式和F在直线BC上得到![]() ,解得t=3.把t=3代入得到F的坐标.
,解得t=3.把t=3代入得到F的坐标.
试题解析:(1)由y=0,得![]() ,解得:
,解得:![]() ,
,![]() ,∴点A的坐标为(-3,0),点B的坐标为(9,0).由x=0,得
,∴点A的坐标为(-3,0),点B的坐标为(9,0).由x=0,得![]() ,∴点C的坐标为(0,
,∴点C的坐标为(0,![]() ).
).
设直线BC的函数表达式为:![]() ,∴
,∴![]() ,解得:
,解得: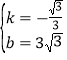 ,∴直线BC的函数表达式为:
,∴直线BC的函数表达式为:![]() ;
;
(2)①过点P作PG⊥x轴于点G .∵A(-3,0),B(9,0),C(0,![]() )∴AO=3,BO=9,OC=
)∴AO=3,BO=9,OC=![]() ,∴tan∠CAO=
,∴tan∠CAO=![]() ,∴∠CAO=60°,∴∠APG=30°,∵AP=t,∴AG=
,∴∠CAO=60°,∴∠APG=30°,∵AP=t,∴AG=![]() ,PG=
,PG=![]() ,∴OG=3-
,∴OG=3-![]() ,∴P(
,∴P(![]() ,
,![]() ).∵OQ=
).∵OQ=![]() ,∴D的横坐标为
,∴D的横坐标为![]() ,∵D在抛物线
,∵D在抛物线![]() 上,∴D的纵坐标为
上,∴D的纵坐标为![]() =
=![]() ,∴D D(
,∴D D(![]() ,
,![]() ).
).
综上所述:P(![]() ,
,![]() ),D(
),D(![]() ,
,![]() );
);
②过点P作PG⊥x轴于点G,PH⊥QD于点H.∵QD⊥x轴,∴四边形PGQH是矩形,∴HQ=PG.∵PQ=PD,PH⊥QD,∴QD=2HQ=2PG.
∵P、D两点的坐标分别为P(![]() ,
,![]() ),D(
),D(![]() ,
,![]() ),∴
),∴![]() =
=![]() ,解得:
,解得:![]() (舍去),
(舍去),![]() ,∴当PQ=PD时,t的值为
,∴当PQ=PD时,t的值为![]() .
.
(3)∵F为PD的中点,且P(![]() ,
,![]() ),D(
),D(![]() ,
,![]() ),由中点坐标公式得:F(
),由中点坐标公式得:F(![]() ,
,![]() ),∵F在直线BC上,∴
),∵F在直线BC上,∴![]() ,∴
,∴![]() ,解得:t=3.
,解得:t=3.
当t=3时,![]() =
=![]() ,
,![]() =
=![]() ,∴F(
,∴F(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
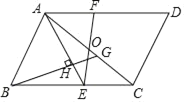
【题目】如图,在平行四边形ABCD中,点O是对角线AC的中点,点E是BC上一点,且AB=AE,连接EO并延长交AD于点F.过点B作AE的垂线,垂足为H,交AC于点G.
(1)若AH=3,HE=1,求△ABE的面积;
(2)若∠ACB=45°,求证:DF=![]() CG.
CG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把所有正偶数从小到大排列,并按如下规律分组:
第一组:2,4;
第二组:6,8,10,12;
第三组:14,16,18,20,22,24
第四组:26,28,30,32,34,36,38,40
……
则现有等式Am=(i,j)表示正偶数m是第i组第j个数(从左到右数),如A10=(2,3),则A2018=( )
A. (31,63) B. (32,17) C. (33,16) D. (34,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点A表示数字6,点B表示数字﹣4
(1)画数轴,并在数轴上标出点A与点B;
(2)数轴上一动点C从点A出发,沿数轴的负方向以每秒2个单位长度的速度移动,经过4秒到达点E,数轴上另一动点D从点B出发,沿数轴的正方向以每秒1个单位长度的速度移动,经过8秒到达点F,求出点E与点F所表示的数,并在第(1)题的数轴上标出点E,点F;
(3)在第(2)题的条件下,在数轴上找出点H,使点H到点E距离与点H到点F距离之和为8,请在数轴上直接标出点H.(不需写出求解过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江津区某玩具商城在“六一”儿童节来临之际,以49元/个的价格购进某种玩具进行销售,并预计当售价为50元/个时,每天能售出50个玩具,且在一定范围内,当每个玩具的售价平均每提高0.5元时,每天就会少售出3个玩具。
(1)若玩具售价不超过60元/个,每天售出玩具总成本不高于686元,预计每个玩具售价的取值范围;
(2)在实际销售中,玩具城以(1)中每个玩具的最低售价及相应的销量为基础,进一步调整了销售方案,将每个玩具的售价提高了![]() %,从而每天的销售量降低了
%,从而每天的销售量降低了![]() %,当每天的销售利润为147元时,求a的值.
%,当每天的销售利润为147元时,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为配合我市创建省级文明城市,某校对八年级各班文明行为劝导志愿者人数进行了统计,各班统计人数有6名、5名、4名、3名、2名、1名共计六种情况,并制作如下两幅不完整的统计图.
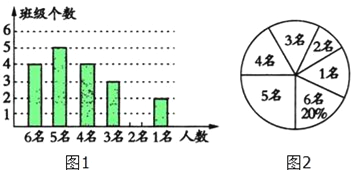
(1)求该年级平均每班有多少文明行为劝导志愿者?并将条形图补充完整;
(2)该校决定本周开展主题实践活动,从八年级只有2名文明行为劝导志愿者的班级中任选两名,请用列表或画树状图的方法,求出所选文明行为劝导志愿者有两名来自同一班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
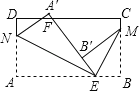
【题目】如图,长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN.
(1)判断直线EN,ME的位置关系,并说明理由;
(2)设∠MEN的平分线EP交边CD于点P,∠MEN的一条三等分线EQ交边CD于点Q.求∠PEQ的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义运算a![]() b=a(1-b),下面给出了关于这种运算的四个结论:
b=a(1-b),下面给出了关于这种运算的四个结论:
①2![]() (-2)=6 ②a
(-2)=6 ②a![]() b=b
b=b![]() a
a
③若a+b=0,则(a![]() a)+(b
a)+(b![]() b)=2ab ④若a
b)=2ab ④若a![]() b=0,则a=0.
b=0,则a=0.
其中正确结论的序号是 (填上你认为所有正确结论的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com