Question

如图，反比例函数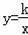（k＞0）与长方形OABC在第一象限相交于D、E两点，OA=2，OC=4，连接OD、OE、DE．记△OAD、△OCE的面积分别为S₁、S₂．

（1）①点B坐标为　　　　　　；②S₁　　　　　　S₂（填“＞”、“＜”、“=”）；

（2）当点D为线段AB的中点时，求k的值及点E坐标；

（3）当S₁+S₂=2时，试判断△ODE的形状，并求△ODE的面积．

Answer 1

【考点】反比例函数综合题．

【分析】（1）根据OA=2，OC=4可直接得到点B坐标；②根据反比例函k的意义可知S₁、S₂都等于|k|，即可得到答案；

（2）当点D为AB中点时，AD=2，得出D的坐标是（2，2），求出解析式即可；

（3）根据当S₁+S₂=2时，由（1）得出S₁=S₂=1，进而得出BD，BE的长，进而得出DO²+DE²=OE²，△ODE是直角三角形，进而得出三角形面积．

【解答】解：（1）①根据长方形OABC中，OA=2，OC=4，

则点B坐标为（4，2），

②∵反比例函数（k＞0）与长方形OABC在第一象限相交于D、E两点，

利用△OAD、△OCE的面积分别为S₁=AD•AO，S₂=•CO•EC，xy=k，得出，

S₁=AD•AO=k，S₂=•CO•EC=k，

∴S₁=S₂；

（2）当点D为AB中点时，AD=2，

∴D的坐标是（2，2），

把D（2，2）代入y=得：

k=2×2=4，

∴y=．

∵点B坐标为（4，2），

∴E点横坐标为：4，

∴4×y=4，

∴y=1，

∴E点坐标为：（4，1）；

（3）当S₁+S₂=2时，∵S₁=S₂，

∴S₁=S₂=1，

∵S₁=AD•AO=AD×2=1，

∴AD=1，

∵S₂=•CO•EC=×4×EC=1，

∴EC=，

∵OA=2，OC=4，

∴BD=4﹣1=3，

BE=2﹣=，

∴DO²=AO²+AD²=4+1=5，

DE²=DB²+BE²=9+=，

OE²=CO²+CE²=16+=，

∴DO²+DE²=OE²，

∴△ODE是直角三角形，

∵DO²=5，

∴DO=，

∵DE²=，

∴DE=，

∴△ODE的面积为：×DO×DE=××=．