
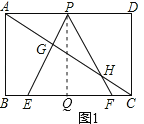
【题目】如图①,在矩形ABCD中,AB=![]() ,BC=3,在BC边上取两点E、F(点E在点F的左边),以EF为边所作等边△PEF,顶点P恰好在AD上,直线PE、PF分别交直线AC于点G、H.
,BC=3,在BC边上取两点E、F(点E在点F的左边),以EF为边所作等边△PEF,顶点P恰好在AD上,直线PE、PF分别交直线AC于点G、H.

(1)求△PEF的边长;
(2)若△PEF的边EF在线段CB上移动,试猜想:PH与BE有何数量关系?并证明你猜想的结论;
(3)若△PEF的边EF在射线CB上移动(分别如图②和图③所示,CF>1,P不与A重合),(2)中的结论还成立吗?若不成立,直接写出你发现的新结论.
【答案】(1)、2;(2)、PH-BE=1、证明过程见解析;(3)、当1<CF<2时,PH=1﹣BE,当2<CF<3时,PH=BE﹣1.
【解析】
试题分析:(1)、过P作PQ⊥BC,垂足为Q,由四边形ABCD为矩形,得到∠B为直角,且AD∥BC,得到PQ=AB,又△PEF为等边三角形,根据“三线合一”得到∠FPQ为30°,在Rt△PQF中,设出QF为x,则PF=2x,由PQ的长,根据勾股定理列出关于x的方程,求出x的值,即可得到PF的长,即为等边三角形的边长;(2)、
PH﹣BE=1,过E作ER垂直于AD,如图所示,首先证明△APH为等腰三角形,在根据矩形的对边平行得到一对内错角相等,可得∠APE=60°,在Rt△PER中,∠REP=30°,根据直角三角形中,30°角所对的直角边等于斜边的一半,由PE求出PR,由PA=PH,则PH﹣BE=PA﹣BE=PA﹣AR=PR,即可得到两线段的关系;(3)、当若△PEF的边EF在射线CB上移动时(2)中的结论不成立,由(2)的解题思路可知当1<CF<2时,PH=1﹣BE,当2<CF<3时,PH=BE﹣1.
试题解析:(1)、过P作PQ⊥BC于Q(如图1), ∵四边形ABCD是矩形, ∴∠B=90°,即AB⊥BC,
又∵AD∥BC, ∴PQ=AB=![]() , ∵△PEF是等边三角形, ∴∠PFQ=60°,
, ∵△PEF是等边三角形, ∴∠PFQ=60°,
在Rt△PQF中,∠FPQ=30°, 设PF=2x,QF=x,PQ=![]() ,根据勾股定理得:
,根据勾股定理得:![]() ,
,
解得:x=1,故PF=2, ∴△PEF的边长为2;
(2)、PH﹣BE=1,理由如下: ∵在Rt△ABC中,AB=![]() ,BC=3, ∴由勾股定理得AC=2
,BC=3, ∴由勾股定理得AC=2![]() ,
,
∴CD=![]() AC, ∴∠CAD=30° ∵AD∥BC,∠PFE=60°, ∴∠FPD=60°, ∴∠PHA=30°=∠CAD,
AC, ∴∠CAD=30° ∵AD∥BC,∠PFE=60°, ∴∠FPD=60°, ∴∠PHA=30°=∠CAD,
∴PA=PH, ∴△APH是等腰三角形, 作ER⊥AD于R(如图2) Rt△PER中,∠RPE=60°, ∴PR=![]() PE=1,
PE=1,
∴PH﹣BE=PA﹣BE=PR=1.
(3)、结论不成立,
当1<CF<2时,PH=1﹣BE, 当2<CF<3时,PH=BE﹣1.



科目:初中数学 来源: 题型:
【题目】已知两个有理数a,b,如果ab<0且a+b>0,那么( )
A. a>0,b>0
B. a<0,b>0
C. a、b同号
D. a、b异号,且正数的绝对值较大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设A、B两镇相距x千米,甲从A镇、乙从B镇同时出发,相向而行,甲、乙行驶的速度分别为u千米/小时、v千米/小时,并有:①出发后30分钟相遇;②甲到B镇后立即返回,追上乙时又经过了30分钟;③当甲追上乙时他俩离A镇还有4千米.求x、u、v.根据题意,由条件③,有四位同学各得到第3个方程如下,其中错误的一个是( )
A.x=u+4
B.x=v+4
C.2x-u=4
D.x-v=4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)一只不透明的袋子中装有4个黑球、2个白球,每个球除颜色外都相同,从中任意摸出3个球,下列事件为必然事件的是( )
A.至少有1个球是黑球
B.至少有1个球是白球
C.至少有2个球是黑球
D.至少有2个球是白球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盒子里有若干个大小相同的白球和红球,从中任意摸出一个球,摸到红球得2分,摸到白球得3分.某人摸到x个红球,y个白球,共得12分.列出关于x、y的二元一次方程:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)在学校组织的科学素养竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为90分,80分,70分,60分,学校将八年级一班和二班的成绩整理并绘制成如下的统计图:

请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在70分及其以上的人数有_____人;
(2)补全下表中空缺的三个统计量:
平均数(分) | 中位数(分) | 众数(分) | |
一班 | 77.6 | 80 | _____ |
二班 | _____ | _____ | 90 |
(3)请根据上述图表对这次竞赛成绩进行分析,写出两个结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com