
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 外接圆的圆心,过点
外接圆的圆心,过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 的切线,交
的切线,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
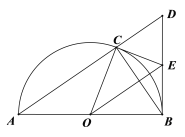
(1)求证:![]() ;
;
(2)填空:①当![]() 的度数为_________时,四边形
的度数为_________时,四边形![]() 为平行四边形;
为平行四边形;
②当![]() 时,
时,![]() 的值为____________.
的值为____________.
【答案】(1)详见解析;(2)①45°;②3.
【解析】
(1)先根据HL证明![]() ,得
,得![]() ,再根据等腰三角形三线合一的性质得出
,再根据等腰三角形三线合一的性质得出![]() ,而已知
,而已知![]() ,问题即得解决;
,问题即得解决;
(2)①由四边形![]() 为平行四边形可得CO∥BD,所以CO⊥BD,进一步即可求出∠A的度数;②由
为平行四边形可得CO∥BD,所以CO⊥BD,进一步即可求出∠A的度数;②由![]() 可得
可得![]() ,然后根据(1)的结论及OA=OB可得
,然后根据(1)的结论及OA=OB可得![]() ,
,
设BE=x,再得出AC与BE的关系即可求出结果.
(1)证明:∵![]() 是
是![]() 的切线,
的切线,![]() ,
,
∴![]() .
.
∵![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
(2)①若四边形![]() 为平行四边形,
为平行四边形,
则CO∥BD.
∵![]() ,
,
∴CO⊥AB,
∵OA=OC,
∴∠A=∠ACO=45°,
所以当![]() 时,四边形
时,四边形![]() 为平行四边形.
为平行四边形.
故答案为45°.
②∵![]() ,∴
,∴![]() ,
,![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() .
.
设BE=x,则BD=2x,AD=4x,
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
故答案为3.


科目:初中数学 来源: 题型:
【题目】小带和小路两个人开车从A城出发匀速行驶至B城.在整个行驶过程中,小带和小路两人车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示.有下列结论;①A,B两城相距300 km;②小路的车比小带的车晚出发1 h,却早到1 h;③小路的车出发后2.5 h追上小带的车;④当小带和小路的车相距50 km时,t=![]() 或t=
或t=![]() .其中正确的结论有( )
.其中正确的结论有( )
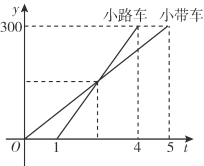
A. ①②③④B. ①②④
C. ①②D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
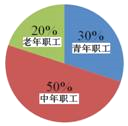
【题目】某单位有职工200人,其中青年职工(20﹣35岁),中年职工(35﹣50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.
为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小张抽样调查单位3名职工的健康指数
年龄 | 26 | 42 | 57 |
健康指数 | 97 | 79 | 72 |
表2:小王抽样调查单位10名职工的健康指数
年龄 | 23 | 25 | 26 | 32 | 33 | 37 | 39 | 42 | 48 | 52 |
健康指数 | 93 | 89 | 90 | 83 | 79 | 75 | 80 | 69 | 68 | 60 |
表3:小李抽样调查单位10名职工的健康指数
年龄 | 22 | 29 | 31 | 36 | 39 | 40 | 43 | 46 | 51 | 55 |
健康指数 | 94 | 90 | 88 | 85 | 82 | 78 | 72 | 76 | 62 | 60 |
根据上述材料回答问题:
小张、小王和小李三人中,谁的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果专卖店5月份销售芒果,采购价为10元![]() ,上旬售价是15元
,上旬售价是15元![]() ,每天可卖出450
,每天可卖出450![]() .市场调查反映:如调整单价,每涨价1元,每天要少卖出50
.市场调查反映:如调整单价,每涨价1元,每天要少卖出50![]() ;每降价1元,每天可多卖出150
;每降价1元,每天可多卖出150![]() .调整价格时也要兼顾顾客利益。
.调整价格时也要兼顾顾客利益。
(1)若专卖店5月中旬每天获得毛利2400元,试求出是如何确定售价的.
(2)请你帮老板算一算,5月下旬如何确定售价每天获得毛利最大,并求出最大毛利.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经纬文教用品商店欲购进A、B两种笔记本,用160元购进的A种笔记本与用240元购进的B种笔记本的数量相同,每本B种笔记本的进价比每本A种笔记本的进价贵10元.
(1)求A、B两种笔记本每本的进价分别为多少元?
(2)若该商店A种笔记本每本售价24元,B种笔记本每本售价35元,准备购进A、B两种笔记本共100本,且这两种笔记本全部售出后总获利高于468元,则最多购进A种笔记本多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.

(1)求该抛物线的解析式;
(2)点![]() 是直线
是直线![]() 上方抛物线上一动点,过点
上方抛物线上一动点,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 平行于
平行于![]() 轴,交
轴,交![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,试求出线段
,试求出线段![]() 的最大值,并写出此时点
的最大值,并写出此时点![]() 的坐标;
的坐标;
(3)抛物线上是否存在一点![]() ,使得
,使得![]() ,若存在,请直接写出点
,若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE⊥AB,交AB的延长线于点E.
(1)求证:CB平分∠ACE;
(2)若BE=![]() ,CE=2,求⊙O的半径.
,CE=2,求⊙O的半径.
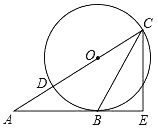
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6的正方形ABCD中,点E、F、G分别在边AB、AD、CD上,EG与BF交于点I,AE=2,BF=EG,DG>AE,则DI的最小值为________.
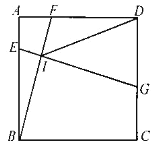
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于A,B两点(A点在B点的左侧),与y轴交于点C,抛物线的对称轴为x=1.
轴交于A,B两点(A点在B点的左侧),与y轴交于点C,抛物线的对称轴为x=1.
(1)求抛物线的表达式;
(2)若CD∥x轴,点D在点C的左侧, ![]() ,求点D的坐标;
,求点D的坐标;
(3)在(2)的条件下,将抛物线在直线x=t右侧的部分沿直线x=t翻折后的图形记为G,若图形G与线段CD有公共点,请直接写出t的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com